题目内容

20．已知各项均为正数的等比数列{an}中，a5•a6=4，则数列{log2an}的前10项和为10．

分析 各项均为正数的等比数列{an}中，a5•a6=4=a1a10=…=a4a7，再利用对数运算性质即可得出．

解答 解：各项均为正数的等比数列{an}中，a5•a6=4=a1a10=…=a4a7，
则数列{log2an}的前10项和=log2（a1a2…•a10）=$lo{g}_{2}{4}^{5}$=10．
故答案为：10．

点评 本题考查了对数运算性质、等比数列的通项公式及其性质，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
16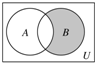．已知全集U=Z，A={x∈Z|x2-x-2＜0}，B={-1，0，1，2}，则图中阴影部分所表示的集合等于（　　）
A．{-1，2}B．{-1，0}C．{0，1}D．{1，2}
17．在直角坐标系xOy中，曲线C1的参数方程为$\left\{\begin{array}{l}{x=2+cosα}\\{y=2+sinα}\end{array}\right.$（α为参数），直线C2的方程为y=$\sqrt{3}x$，以O为极点，以x轴正半轴为极轴建立极坐标系，
（1）求曲线C1和直线C2的极坐标方程；
（2）若直线C2与曲线C1交于A，B两点，求$\frac{1}{|OA|}$+$\frac{1}{|OB|}$．
8．在锐角△ABC中，角A，B，C的对边分别为a，b，c，且（2b-c）cosA=acosC．
（1）求角A的大小；
（2）若y=cos2$\frac{B}{2}$+cos2$\frac{C}{2}$-1，求y的取值范围．
15．将A，B，C，D，E排成一列，要求A，B，C在排列中顺序为“A，B，C”或“C，B，A”（ A，B，C可以不相邻），这样的排列数有（　　）
A．12种B．20种C．40种D．60种
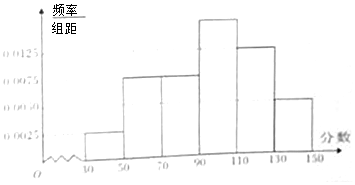5．某市举行“中学生诗词大赛”海选，规定：成绩大于或等于90分的具有参赛资格．某校有800名学生参加了海选，所有学生的成绩均在区间[30，150]内，其频率分布直方图如图：
（Ⅰ）求获得参赛资格的人数；
（Ⅱ）若大赛分初赛和复赛，在初赛中每人最多有5次选题答题的机会，累计答对3题或答错3题即终止，答对3题者方可参加复赛．已知参赛者甲答对每一个问题的概率都相同，并且相互之间没有影响，已知他连续两次答错的概率为$\frac{1}{9}$，求甲在初赛中答题个数X的分布列及数学期望E（X）
12．已知关于x的不等式|x-1|+|x+3|≤m的解集不是空集，记m的最小值为t．
（Ⅰ）求t的值；
（Ⅱ）若不等式|x-1|+|x+3|＞|x-a|的解集包含[-1，0]，求实数a的取值范围．
9．已知集合U={x|x＞1}，集合A={x|x2-4x+3＜0}，则∁UA=（　　）
A．[3，+∞）B．（3，+∞）C．（-∞，-1）D．（1，3）
10．已知实数x、y满足$\left\{{\begin{array}{l}{x+y≥2}\\{x-y≤2}\\{0≤y≤3}\end{array}}\right.$，则z=2x+y-6的最小值是-5．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网