题目内容
3.已知M,F为椭圆的$C:\frac{x^2}{20}+\frac{y^2}{16}=1$的上顶点和右焦点,直线l与椭圆C交与A,B两点,且三角形△MAB的重心恰为F,则直线l的方程为6x-5y-28=0.分析 设B(x1,y1),A(x2,y2),求出椭圆的右焦点为(2,0),利用三角形的重心坐标,推出x1+x2=6,y1+y2=-4,利用平方差法,求出直线的斜率,求出直线的中点坐标,利用点斜式求解直线方程.
解答 解:设B(x1,y1),A(x2,y2),椭圆的$C:\frac{x^2}{20}+\frac{y^2}{16}=1$的右焦点为(2,0)
∵点M(0,4),且椭圆右焦点F2恰为△ABC的重心
∴$\frac{{x}_{1}+{x}_{2}+0}{3}=2$,$\frac{{y}_{1}+{y}_{2}+4}{2}=0$
∴x1+x2=6,y1+y2=-4 ①
∵$\frac{{{x}_{1}}^{2}}{20}+\frac{{{y}_{1}}^{2}}{16}=1$,$\frac{{{x}_{2}}^{2}}{20}+\frac{{{y}_{2}}^{2}}{16}=1$
∴两式相减得:$\frac{({x}_{1}+{x}_{2})({x}_{1}-{x}_{2})}{20}+\frac{({y}_{1}+{y}_{2})({y}_{1}+{y}_{2})}{16}=0$,
将①代入得:$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=$\frac{6}{5}$,即直线l的斜率为k=$\frac{6}{5}$
∵直线l 过BA中点(3,-2)
∴直线l的方程为y+2=$\frac{6}{5}$(x-3)
故答案为:6x-5y-28=0.
点评 本题考查直线与椭圆方程的综合应用,点差法的应用,考查转化思想以及计算能力.

练习册系列答案
相关题目
14.如图,在长方形OABC内任取一点P(x,y),则点P落在阴影部分的概率为( )

| A. | $1-\frac{3}{2e}$ | B. | $1-\frac{1}{2e}$ | C. | $1-\frac{2}{e}$ | D. | $1-\frac{1}{e}$ |
11.已知$\frac{1+2i}{a+bi}$=2-i(i为虚数单位,a,b∈R),在|a-bi|=( )
| A. | -i | B. | 1 | C. | 2 | D. | $\sqrt{5}$ |
12. 如图,在正方形网格纸上,粗实线画出的是某多面体的三视图及其部分尺寸,若该多面体的顶点在同一球面上,则该球的表面积等于( )
如图,在正方形网格纸上,粗实线画出的是某多面体的三视图及其部分尺寸,若该多面体的顶点在同一球面上,则该球的表面积等于( )
 如图,在正方形网格纸上,粗实线画出的是某多面体的三视图及其部分尺寸,若该多面体的顶点在同一球面上,则该球的表面积等于( )
如图,在正方形网格纸上,粗实线画出的是某多面体的三视图及其部分尺寸,若该多面体的顶点在同一球面上,则该球的表面积等于( )| A. | 8π | B. | 18π | C. | 24π | D. | 8$\sqrt{6}$π |
13.命题“?x∈R,使得x2<1”的否定是( )
| A. | ?x∈R,都有x2<1 | B. | ?x∈R,使得x2≥1 | ||
| C. | ?x∈R,都有x≤-1或x≥1 | D. | ?x∈R,使得x2>1 |
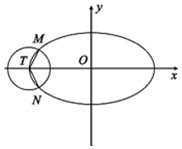 如图已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,以椭圆的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0),设圆T与椭圆C交于点M,N.
如图已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,以椭圆的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0),设圆T与椭圆C交于点M,N.