题目内容
函数y=sinθcos2θ在0<θ<
范围内的最大值是( )
| π |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:三角函数的最值
专题:三角函数的图像与性质,不等式的解法及应用
分析:要求表达式的最大值需要平方后,利用均值不等式求解即可.
解答:
解:函数y=sinθcos2θ在0<θ<
范围内的最大值,
就是求解y2=[sinθcos2θ]2在0<θ<
范围内的最大值再开方,
∴2y2=2sin2θcos2θcos2θ≤(
)3=
,
此时2sin2θ=cos2θ,即tan2θ=
,满足0<θ<
,
2y2≤
,
∴y≤
.
故选:A.
| π |
| 2 |
就是求解y2=[sinθcos2θ]2在0<θ<
| π |
| 2 |
∴2y2=2sin2θcos2θcos2θ≤(
| 2sin2θ+cos2θ+cos2θ |
| 3 |
| 8 |
| 27 |
此时2sin2θ=cos2θ,即tan2θ=
| 1 |
| 2 |
| π |
| 2 |
2y2≤
| 8 |
| 27 |
∴y≤
2
| ||
| 9 |
故选:A.
点评:本题考查三角函数的最值的求法,均值不等式的应用,考查转化思想以及计算能力.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
执行如图所示的程序框图,如果输出的结果为
,则判断框内应填入的条件是( )
| 15 |
| 8 |

| A、k<3 | B、k>3 |
| C、k<4 | D、k>4 |
已知变量x、y满足约束条件
,则z=2x+y的最小值为( )
|
| A、0 | B、1 | C、3 | D、4 |
已知定义在R上的奇函数f(x),其导函数为f′(x),当x∈(0,+∞)时,恒有xf′(x)<f(-x).若g(x)=xf(x),则满足g(1)>g(1-2x)的实数x的取值范围是( )
| A、(0,1) |
| B、(-∞,0)∪(1,+∞) |
| C、(0,+∞) |
| D、(-∞,0) |
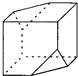
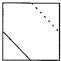
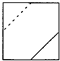
某四棱锥的三视图如图所示,则最长的一条侧棱长度为( )


A、
| ||
B、
| ||
C、
| ||
D、
|