题目内容
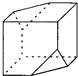
将一个正方体沿其棱的中点截去两三个棱锥后所得几何体如图所示，则其俯视图为（ ）
A、 |
B、 |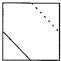
C、 |
D、 |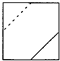
考点：简单空间图形的三视图
专题：空间位置关系与距离
分析：根据正方体的几何特征，分析几何体俯视图外轮廓的形状及截面截正方体表面所得的棱能否看到，进而得到答案．
解答：
解：将一个正方体沿其棱的中点截去两三个棱锥后所得几何体的俯视图满足：
外轮廓是一个正方形，
左上角能看到上底面被截面所成的棱，为实线，
右下角看不到下底面被截面所成的棱，为虚线，
故选：C．
外轮廓是一个正方形，
左上角能看到上底面被截面所成的棱，为实线，
右下角看不到下底面被截面所成的棱，为虚线，
故选：C．
点评：本题考查考生对空间立体图及平面图射影的抽象考察，熟练掌握三视图的画法是解答的关键．
练习册系列答案
相关题目
函数y=sinθcos2θ在0＜θ＜
范围内的最大值是（ ）
| π |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在花园小区内有一块三边长分别为3米、4米、5米的三角形绿化地，有一只小狗在其内部玩耍，若不考虑小狗的大小，则在任意指定的某时刻，小狗与三角形三个顶点的距离均超过1米的概率是（ ）
A、1-
| ||
B、1-
| ||
C、2-
| ||
D、2-
|
已知集合A={-1，0，1}，B={x|
＜2x＜4}，则A∩B=（ ）
| 1 |
| 2 |
| A、{1} |
| B、{-1，1} |
| C、{0，1} |
| D、{-1，0，1} |
已知集合M={x|-1≤x＜2}，N={x|x-a≤0}，若M∩N≠∅，则a的取值范围是（ ）
| A、（-∞，2] |
| B、（-1，+∞） |
| C、[-1，+∞） |
| D、[-1，1] |
在△ABC中，AD为BC边上的高，已知：AC=b；AB=c，AD=BC，求