题目内容
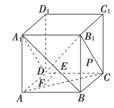
如图,在四面体PABC中,PC⊥AB,PA⊥BC,点D,E,F,G分别是棱AP,AC,BC,PB的中点.
(1)求证:DE∥平面BCP;
(2)求证:四边形DEFG为矩形;
(3)是否存在点Q,到四面体PABC六条棱的中点的距离相等?说明理由.
解:
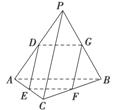
(1)证明:因为D,E分别为AP,AC的中点,所以DE∥PC.
又因为DE⊄平面BCP,
所以DE∥平 面BCP.
面BCP.
(2)证明:因为D,E,F,G分别为AP,AC,BC,PB的中点,
所以DE∥PC∥FG,DG∥AB∥EF,
所以四边形DEFG 为平行四边形.
为平行四边形.
又因为PC⊥AB,
所以DE⊥DG,
所以四边形DEFG为矩形.
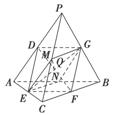
(3)存在点Q满足条件,理由如下:
连接DF,EG,设Q为EG的中点.
由(2)知,DF∩EG=Q,且QD=QE=QF=QG=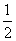 EG.
EG.
分别取PC,AB的中点M,N,连接ME,EN,NG,MG,MN.
与(2)同理,可证四边形MENG为矩形,其对角线交点为EG的中点Q,
且QM=QN=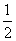 EG,
EG,
所以Q为满足条件的点.

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案若某产品的直径长与标准值的差的绝对值不超过1 mm时,则视为合格品,否则视为不合格品.在近期一次产品抽样检查中,从某厂生产的此种产品中,随机抽取5000件进行检测,结果发现有50件不合格品.计算这50件不合格品的直径长与标准值的差(单位:mm),将所得数据分组 ,得到如下频率分布表:
,得到如下频率分布表:
| 分组 | 频数 | 频率 |
| [-3,-2) |
| 0.10 |
| [-2,-1) | 8 | |
| (1,2] |
| 0.50 |
| (2,3] | 10 | |
| (3,4] | ||
| 合计 | 50 | 1.00 |
(1)将上面表格中缺少的数据填在相应位置;
(2)估计该厂生产的此种产品中,不合格品的直径长与标准值的差落在区间(1,3]内的概率;
(3)现对该厂这种产品的某个批次进行检查,结果发现有20件不合格品.据此估算这批产品中的合格品的件数.
 及其边界上运动,并且总保持AP⊥BD1,则动点P的轨迹是( )
及其边界上运动,并且总保持AP⊥BD1,则动点P的轨迹是( )
 ____.
____.