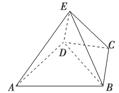
题目内容
如图，几何体E－ABCD是四棱锥，△ABD为正三角形，CB＝CD，EC⊥BD.
(1)求证：BE＝DE；
(2)若∠BCD＝120°，M为线段AE的中点，求证：DM∥平面BEC.
证明：
(1)如图，取BD的中点O，连接CO，EO.
由于CB＝CD，所以CO⊥BD，
又EC⊥BD，EC∩CO＝C，
CO，EC⊂平面EOC，
所以BD
⊥平面EOC，
因此BD⊥EO，
又O为BD的中点，
所以BE＝DE.
(2)法一：如图，取AB的中点N，
连接DM，DN，MN.
因为M是AE的中点，
所以MN∥BE.
又MN⊄平面BEC，BE⊂平面BEC，
所以MN∥平面BEC.
又因为△ABD为正三角形，
所以∠BDN＝30°.
又CB＝CD，∠BCD＝120°，
因此∠CBD＝30°，
所以DN∥BC.
又DN⊄平面BEC，BC⊂平面BEC，
所以DN∥平面BEC.
又MN∩DN＝N，
故平面DMN∥平面BEC.
又DM⊂平面DMN，
所以DM∥平面BEC.
法二：如图，延长AD，BC交于点F，连接EF.
因为CB＝CD，∠BCD＝120°，
所以∠CBD＝30°.
因为△ABD为正三角形，
所以∠BAD＝60°，∠ABC＝90°，
因此∠AFB＝30°，
所以AB＝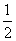
AF.
又AB＝AD，
所以D为线段AF的中点．
连接DM，由于点M是线段AE的中点，
因此DM∥EF.
又DM⊄平面BEC，EF⊂平面BEC，
所以DM∥平面BE
C.
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
是函数f(x)的一个零点；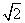
，则此球的体积为( )
π B．4
π
下列四个命题中：①若l⊂α，C∈α，则C∈l；②若A∈l，B∈l，且B∈/ α，则l⊂/ α；③若l⊂α，C∈l，则C∈α；④若l⊂/ α，C∈l，则C∈/ α.正确的命题有________(把所有正确命题的序号都填上)．
②若α⊥γ，β⊥γ，则α∥β；
2)，C(－3,0,4)，设a＝
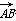，b＝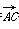
.
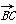，求向量c的坐标；