题目内容
已知函数f(x)=1-
,定义域为(-1,+∞),且f(2)=-1
(1)求m的值;
(2)试判断函数f(x)在定义域上的单调性,并用定义加以证明;
(3)在定义域内利用单调性解不等式f(x)<-1.
| m |
| x+1 |
(1)求m的值;
(2)试判断函数f(x)在定义域上的单调性,并用定义加以证明;
(3)在定义域内利用单调性解不等式f(x)<-1.
考点:函数单调性的判断与证明,函数单调性的性质
专题:函数的性质及应用
分析:(1)把点代入求出即可,(2)设x1>x2>-1,根据定义直接证明,(3)根据不等式的解题步骤解出即可.
解答:
解:(1)把(2,-1)代入函数得:-1=1-
,解得:m=6;
(2)设x1>x2>-1,
∴f(x1)-f(x2)=1-
-1+
=
,
∵x1-x2>0,x2+1>0,x1+1>0,
∴f(x1)-f(x2)>0,
即:f(x1)>f(x2),
∴函数f(x)在定义域上是增函数;
(3)解1-
<-1,
即
>2,
解得:x<2,
∴-1<x<2.
∴不等式的解集为:{x|-1<x<2}.
| m |
| 3 |
(2)设x1>x2>-1,
∴f(x1)-f(x2)=1-
| m |
| x1+1 |
| m |
| x2+1 |
=
| m(x1-x2) |
| (x2+1)(x1+1) |
∵x1-x2>0,x2+1>0,x1+1>0,
∴f(x1)-f(x2)>0,
即:f(x1)>f(x2),
∴函数f(x)在定义域上是增函数;
(3)解1-
| 6 |
| x+1 |
即
| 6 |
| x+1 |
解得:x<2,
∴-1<x<2.
∴不等式的解集为:{x|-1<x<2}.
点评:本题考察了用定义证明函数的单调性,不等式的解法,是一道基础题.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
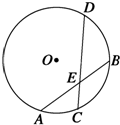 如图所示,已知⊙O的半径为5,两弦AB、CD相交于AB的中点E,且AB=8,CE:ED=4:9,则圆心到弦CD的距离为( )
如图所示,已知⊙O的半径为5,两弦AB、CD相交于AB的中点E,且AB=8,CE:ED=4:9,则圆心到弦CD的距离为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
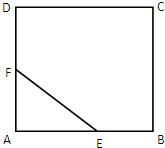 如图,有一块正方形区域ABCD,现在要划出一个直角三角形AEF区域进行绿化,满足:EF=1米,设角AEF=θ,θ∈[
如图,有一块正方形区域ABCD,现在要划出一个直角三角形AEF区域进行绿化,满足:EF=1米,设角AEF=θ,θ∈[