Question

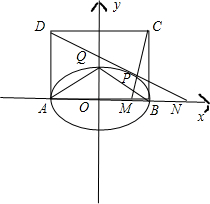
如图A、B分别是椭圆圆

x2

a2

+

y2

b2

=1（a＞b＞0）的左右顶点，以AB为边作正方形ABCD，若Q是椭圆的上顶点，△QAB与正方形ABCD的面积之比为

1

8

，求椭圆的离心率

Answer 1

考点：椭圆的简单性质

专题：计算题,圆锥曲线的定义、性质与方程

分析：运用椭圆的性质和三角形及正方形的面积公式，可得a=2b，再由a，b，c的关系和离心率公式，即可计算得到．

解答： 解：由椭圆的性质可得，|AB|=2a，|OQ|=b，
则△QAB与正方形ABCD的面积之比为

1

8

，
即为

1 2 •2ab

4a2

=

1

8

，即a=2b，
则c=

a2-b2

=

3

2

a，
即有e=

c

a

=

3

2

则椭圆的离心率为

3

2

．

点评：本题考查椭圆的方程和性质，考查椭圆离心率的求法，考查面积公式的运用，属于基础题．