题目内容
若不等式
≤ax+2a恒成立，则实数a的取值范围为 ．
| -x2+4x |
考点：函数恒成立问题
专题：函数的性质及应用,不等式的解法及应用
分析：令y=f（x）=
，在同一直角坐标系中作出f（x）=
与y=ax+2a=a（x+2）的图象，数形结合，分析即可求得实数a的取值范围．
| -x2+4x |
| -x2+4x |
解答：
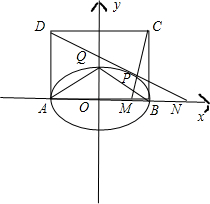
解：令y=f（x）=
，则（x-2）2+y2=4（0≤x≤4），是以（2，0）为圆心，2为半径的上半圆．
令y=ax+2a=a（x+2），是以a为斜率，且过定点（-2，0）的直线，
作图如下：
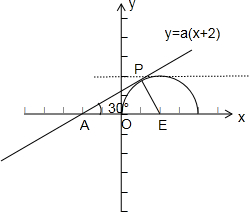
由图可知，当直线y=a（x+2）与半圆f（x）=
相切时，由Rt△AEP中AE=4，PE=2知，∠PAE=30°，
所以，a=kPA=tan30°=
，此时满足不等式
≤ax+2a恒成立，
将此时的直线l（直线AP）绕定点A逆时针方向旋转，直到与x轴垂直，在这个过程中，不等式
≤ax+2a恒成立，
所以，a≥
．
故答案为：[
，+∞）．
| -x2+4x |
令y=ax+2a=a（x+2），是以a为斜率，且过定点（-2，0）的直线，
作图如下：
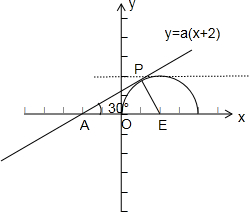
由图可知，当直线y=a（x+2）与半圆f（x）=
| -x2+4x |
所以，a=kPA=tan30°=
| ||
| 3 |
| -x2+4x |
将此时的直线l（直线AP）绕定点A逆时针方向旋转，直到与x轴垂直，在这个过程中，不等式
| -x2+4x |
所以，a≥
| ||
| 3 |
故答案为：[
| ||
| 3 |
点评：本题考查函数恒成立问题，在同一直角坐标系中作出f（x）=
与y=ax+2a=a（x+2）的图象是关键，考查数学结合思想与等价转化思想的综合运用，属于中档题．
| -x2+4x |
练习册系列答案
相关题目
已知向量
=(-1，2)，
=(2，x)，
=(x，-3)，若
∥
，则|
|等于（ ）
| a |
| b |
| c |
| a |
| b |
| c |
A、
| ||
| B、10 | ||
C、
| ||
| D、5 |
若a+
=1-bi（a、b是实数，i是虚数单位），则复数z=a+bi对应的点在（ ）
| 1 |
| i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
集合A={x∈R|y=log2（x-4）}，B={x∈R|y=
}，则A∩B=（ ）
| ||
| x-5 |
| A、（4，+∞） |
| B、（4，5）∪（5，+∞） |
| C、[4，5）∪（5，+∞） |
| D、[4，+∞） |
已知集合A={-2，0，1，3，5}，B={x∈N|-2＜x≤4}，则A∩B=（ ）
| A、{1，3} |
| B、{0，1，3} |
| C、{-1，0，1，3} |
| D、{-1，0，1，2，3，4，5} |
已知f（x）是定义在R上的函数，且f（x）的图象关于坐标原点对称；当x＜0时，f（x）=-x2+2015x．若f（2-a2）+f（a）＜0，则实数a的取值范围是（ ）
| A、（-∞，-1）∪（2，+∞） |
| B、（-∞，-2）∪（1，+∞） |
| C、（-1，2） |
| D、（-2，1） |
