题目内容
已知sinx+cosx=-
(0<x<π),求tanx的值.
| 1 |
| 5 |
考点:同角三角函数基本关系的运用
专题:计算题,三角函数的求值
分析:先根据sinx+cosx的值和二者的平方关系联立求得sinx、cosx的值,进而利用商数关系求得tanx的值.
解答:
解:∵sinx+cosx=-
(0<x<π),
∴两边平方得2sinxcosx=-
,cosx<0
∴(sinx-cosx)2=1-2sinxcosx=
,
∵sinx-cosx>0,
∴sinx-cosx=
,
与sinx+cosx=-
联立解得sinx=
,cosx=-
,
∴tanx=
=-
.
| 1 |
| 5 |
∴两边平方得2sinxcosx=-
| 24 |
| 25 |
∴(sinx-cosx)2=1-2sinxcosx=
| 49 |
| 25 |
∵sinx-cosx>0,
∴sinx-cosx=
| 7 |
| 5 |
与sinx+cosx=-
| 1 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
∴tanx=
| sinx |
| cosx |
| 3 |
| 4 |
点评:本题主要考查了同角三角函数的基本关系的应用.解题的过程中要特别注意根据角的范围确定三角函数值的正负号.

练习册系列答案
相关题目
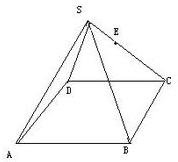 在底面是菱形的四棱锥S-ABCD中,SA=SC=2a,SB=SD=
在底面是菱形的四棱锥S-ABCD中,SA=SC=2a,SB=SD=