题目内容
在平面直角坐标系中，O为坐标原点，A、B、C三点满足
=-
+2
．
（1）试用
表示
；
（2）已知A（1，cosx），B（1+sinx，cosx），x∈[0，
]，f（x）=
•
-2（m2+1）|
|的最小值为
，求实数m的值．
| OC |
| OA |
| OB |
（1）试用
| AB |
| AC |
（2）已知A（1，cosx），B（1+sinx，cosx），x∈[0，
| π |
| 2 |
| OA |
| OC |
| AB |
| 1 |
| 2 |
考点：平面向量数量积的运算
专题：综合题,平面向量及应用
分析：（1）由
=-
+2
，得
-
=-
+
，利用减法的三角形法则可得结果；
（2）根据向量的线性运算、数量积运算可得f（x）=-sin2x-2m2sinx+2，令t=sinx，则可化为二次函数，由二次函数的性质可得最小值，令其为
可求m．
| OC |
| OA |
| OB |
| OC |
| OB |
| OA |
| OB |
（2）根据向量的线性运算、数量积运算可得f（x）=-sin2x-2m2sinx+2，令t=sinx，则可化为二次函数，由二次函数的性质可得最小值，令其为
| 1 |
| 2 |
解答：
解：（1）由
=-
+2
，得
-
=-
+
，即
=
．
∴
-
=
，
∴
=2
．
（2）
=-
+2
=（-1，-cosx）+2（1+sinx，cosx）=（2sinx+1，cosx），
•
=（1，cosx）•（2sinx+1，cosx）=2sinx+1+cos2x，|AB|=sinx，
∴f（x）=
•
-2（m2+1）|
|=2sinx+1+cos2x-2（m2+1）sinx，
=-sin2x-2m2sinx+2，
令t=sinx，∵x∈[0，
]，∴t∈[0，1]，
则-sin2x-2m2sinx+2=-t2-2m2t+2在[0，1]上单调递减，
∴f（x）的最小值为-1-2m2+2=
，即m2=
，
∴m=±
．
| OC |
| OA |
| OB |
| OC |
| OB |
| OA |
| OB |
| BC |
| AB |
∴
| AC |
| AB |
| AB |
∴
| AC |
| AB |
（2）
| OC |
| OA |
| OB |
| OA |
| OC |
∴f（x）=
| OA |
| OC |
| AB |
=-sin2x-2m2sinx+2，
令t=sinx，∵x∈[0，
| π |
| 2 |
则-sin2x-2m2sinx+2=-t2-2m2t+2在[0，1]上单调递减，
∴f（x）的最小值为-1-2m2+2=
| 1 |
| 2 |
| 1 |
| 4 |
∴m=±
| 1 |
| 2 |
点评：本题考查平面向量的线性运算、数量积运算、二次函数的性质，属中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在△ABC中，A，B，C所对的边分别是a，b，c，满足3a2+3b2=c2+4ab，现设f（x）=tanx，则（ ）
| A、f（sinA）≤f（cosB） |
| B、f（sinA）≥f（cosB） |
| C、f（sinA）≤f（sinB） |
| D、f（cosA）≤f（cosB） |
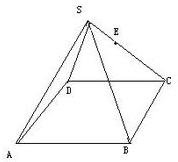在底面是菱形的四棱锥S-ABCD中，SA=SC=2a，SB=SD=