Question

12．设P为椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1上一点，F为椭圆的右焦点，A（2，2），则|PA|-|PF|的最小值为$\sqrt{13}$-4．

Answer 1

分析 由题意作图辅助，通过椭圆的定义转化为求|PA|+|PF₁|-4的最小值，从而解得．

解答 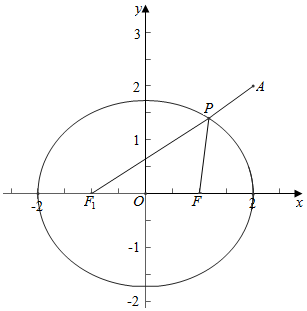解：由题意作图象如右图，
∵椭圆的方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1，
∴a=2，c=1，b=$\sqrt{3}$；
∴|PF|+|PF₁|=4，
∴|PA|-|PF|=|PA|-（4-|PF₁|）
=|PA|+|PF₁|-4，
故|PA|+|PF₁|的最小值为$\sqrt{（2+1）^{2}+{2}^{2}}$=$\sqrt{13}$，
故|PA|-|PF|的最小值为$\sqrt{13}$-4，
故答案为：$\sqrt{13}$-4．

点评 本题考查了圆锥曲线的定义，同时考查了转化思想与数形结合的思想方法的应用．