题目内容
8.在平面直角坐标系中,不等式组$\left\{\begin{array}{l}{y≥x+2}\\{x+y≤2}\\{2x+y≥0}\end{array}\right.$表示的平面区域的面积是$\frac{4}{3}$,若函数y=|2x+m|与该区域有公共点,则实数m的取值范围是[-2,0]∪[2,8].分析 由题意作平面区域,从而可得B(-$\frac{2}{3}$,$\frac{4}{3}$),A(-2,4),D(0,2),C(-1,2);从而求面积;结合图象可得求4=|-4+m|,|m|=2的根,从而求得.
解答 解:由题意作平面区域如下(图1),
由$\left\{\begin{array}{l}{y=x+2}\\{y=-2x}\end{array}\right.$解得,x=-$\frac{2}{3}$,y=-$\frac{2}{3}$+2=$\frac{4}{3}$,故B(-$\frac{2}{3}$,$\frac{4}{3}$);
由$\left\{\begin{array}{l}{y=2-x}\\{y=-2x}\end{array}\right.$解得,x=-2,y=4,故A(-2,4);
易知D(0,2),C(-1,2);
故S=$\frac{1}{2}$•1•(4-$\frac{4}{3}$)=$\frac{4}{3}$;
由题意作平面区域如下(图2),
当过点A(-2,4)时,4=|-4+m|,
解得,m=8或m=0;
当过点D(0,2)时,|m|=2,
解得,m=-2或m=2;
结合图象可知,-2≤m≤0或2≤m≤8;
故答案为:$\frac{4}{3}$,[-2,0]∪[2,8].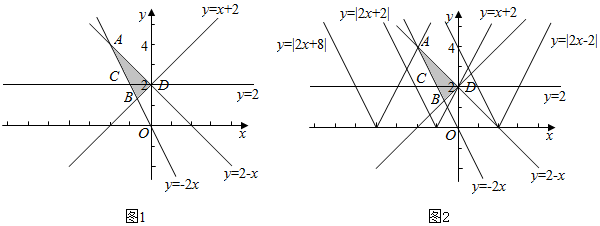
点评 本题考查了线性规划,同时考查了学生的作图能力及数形结合的思想方法的应用及分类讨论的思想应用.

练习册系列答案
相关题目
1.某空间几何体的三视图如图所示,则该几何体的体积为( )


| A. | 128 | B. | $\frac{128}{3}$ | C. | $\frac{64}{3}$ | D. | $\frac{32}{3}$ |
16.下列函数是偶函数,且在[0,1]上单调递增的是( )
| A. | y=sin(x+$\frac{π}{2}$) | B. | y=-cos4x | C. | y=-x2 | D. | y=|sin(π+x)| |
17.已知集合M={-2,-1,0,1,2},N={x|(x+1)(x-2)<0},则M∩N=( )
| A. | {-1,0} | B. | {0,1} | C. | {-1,0,1} | D. | {0,1,2} |