题目内容
17.在数列{an}中,a1=$\frac{3}{2}$,2an=an-1+6n-3,求通项an.分析 2an=an-1+6n-3,变形为:an-(6n-9)=$\frac{1}{2}$[an-1-(6n-15)],利用等比数列的通项公式即可得出.
解答 解:∵2an=an-1+6n-3,
变形为:an-(6n-9)=$\frac{1}{2}$[an-1-(6n-15)],
∴数列{an-(6n-9)}是等比数列,首项为-$\frac{3}{2}$,公比为$\frac{1}{2}$.
∴an-(6n-9)=$-\frac{3}{2}$×$(\frac{1}{2})^{n-1}$=-3×$(\frac{1}{2})^{n}$.
∴an=(6n-9)-3×$(\frac{1}{2})^{n}$.
点评 本题考查了等比数列的通项公式、递推关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
 .
. 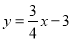 与
与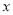 轴、
轴、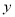 轴分别交于
轴分别交于 两点,
两点,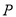 是以
是以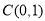 为圆心,1为半径的圆上一动点,连结
为圆心,1为半径的圆上一动点,连结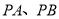 ,则
,则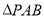 面积的最大值是( )
面积的最大值是( )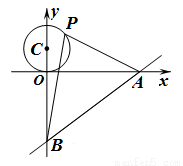
 D.
D.