题目内容
6.已知圆C过坐标原点,面积为2π,且与直线l:x-y+2=0相切,则圆C的方程是(x+$\sqrt{2}$)2+(y+$\sqrt{2}$)2=2或(x-$\sqrt{2}$)2+(y-$\sqrt{2}$)2=2.分析 设圆心坐标为(a,b),利用圆C过坐标原点,面积为2π,且与直线l:x-y+2=0相切,求出a,b,即可求出圆C的方程.
解答 解:设圆心坐标为(a,b),则
∵面积为2π,∴半径r=$\sqrt{2}$,
∵圆C过坐标原点,且与直线l:x-y+2=0相切,
∴$\sqrt{{a}^{2}+{b}^{2}}$=$\frac{|a-b+2|}{\sqrt{2}}$=$\sqrt{2}$,
∴a=b=$±\sqrt{2}$,
∴圆C的方程是(x+$\sqrt{2}$)2+(y+$\sqrt{2}$)2=2或(x-$\sqrt{2}$)2+(y-$\sqrt{2}$)2=2.
故答案为:(x+$\sqrt{2}$)2+(y+$\sqrt{2}$)2=2或(x-$\sqrt{2}$)2+(y-$\sqrt{2}$)2=2.
点评 本题考查的是圆的方程,考查直线与圆的位置关系,考查学生的计算能力,利用条件建立方程,求出圆心与半径是解题的关键所在.

练习册系列答案
相关题目
15.若a=log0.20.3,b=log0.30.2,c=1,则a,b,c的大小关系是( )
| A. | a>b>c | B. | b>a>c | C. | b>c>a | D. | c>b>a |
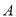 型和20台
型和20台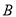 型电脑的利润为4000元,销售20台
型电脑的利润为4000元,销售20台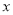 台,这100台电脑的销售总利润为
台,这100台电脑的销售总利润为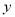 元.
元.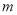 (
(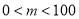 )元,且限定商店最多购进
)元,且限定商店最多购进