题目内容
1.在△ABC中,角A,B,C的对边分别为a,b,c,若b=5,a=3,cos(B-A)=$\frac{7}{9}$,则△ABC的面积为( )| A. | $\frac{15}{2}$ | B. | $\frac{5\sqrt{2}}{3}$ | C. | 5$\sqrt{2}$ | D. | 2$\sqrt{2}$ |
分析 作∠ABD=∠A,交AC于D,设AD=BD=x,则CD=5-x,利用余弦定理求出x,进而可得cosC,sinC,利用三角形的面积公式可得结论.
解答 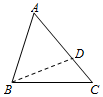 解:作∠ABD=∠A,交AC于D,设AD=BD=x,则CD=5-x,
解:作∠ABD=∠A,交AC于D,设AD=BD=x,则CD=5-x,
∵a=3,cos(B-A)=$\frac{7}{9}$,
∴(5-x)2=x2+9-2×3×x×$\frac{7}{9}$,
∴x=3,
∴CD=2,BD=3,
∴cosC=$\frac{4+9-9}{2×2×3}$=$\frac{1}{3}$,
∴sinC=$\frac{2\sqrt{2}}{3}$,
∴△ABC的面积为$\frac{1}{2}×3×5×\frac{2\sqrt{2}}{3}$=5$\sqrt{2}$.
故选:C.
点评 本题考查三角形面积的计算,考查余弦定理的运用,解题的关键是正确运用余弦定理求出cosC.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
15.若a=log0.20.3,b=log0.30.2,c=1,则a,b,c的大小关系是( )
| A. | a>b>c | B. | b>a>c | C. | b>c>a | D. | c>b>a |
 中,其频率分布直方图如图所示,则在抽测的200辆汽车中,时速在区间
中,其频率分布直方图如图所示,则在抽测的200辆汽车中,时速在区间 内的汽车有 辆.
内的汽车有 辆.