Question

13．若变量x、y满足约束条件$\left\{\begin{array}{l}2x+y-2≥0\\ x+y-2≤0\\ x-y≥0\end{array}\right.$，则$\frac{x+1}{x+y+1}$的最小值为$\frac{1}{3}$．

Answer 1

分析 首先画出可行域，化简目标函数，通过区域内的点与定点（-1，0）连接的直线的斜率解答即可．

解答 解：画出变量x、y满足约束条件$\left\{\begin{array}{l}2x+y-2≥0\\ x+y-2≤0\\ x-y≥0\end{array}\right.$，的可行域如图：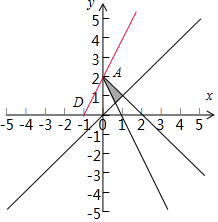

目标函数$\frac{x+1}{x+y+1}$=$\frac{1}{1+\frac{y}{x+1}}$，$\frac{y}{x+1}$的几何意义是过区域内的点与定点（-1，0）
连接的直线的斜率，
斜率最大值时，则$\frac{x+1}{x+y+1}$取得最小值，
由其几何意义得到A与D（-1，0）连接的直线斜率最大，
所以最小值为$\frac{0+1}{0+2+1}$=$\frac{1}{3}$；
故答案为：$\frac{1}{3}$．

点评 本题考查了可行域的画法以及利用目标函数的几何意义求最值；本题解答的关键是明确目标函数的几何意义．