��Ŀ����
��֪����{an}�У�a1=2��a2=3����ǰn���Sn����Sn+1+Sn-1=2Sn+1��n��2��n��N*����
��1����֤������{an}Ϊ�Ȳ����У�����{an}��ͨ�ʽ��
��2����bn=2n•an��������{bn}��ǰn���Tn��
��3����Cn=4n+��-1��n-1•��2an����Ϊ����������n��N*�����Ƿ����ȷ���˵�ֵ��ʹ�ö�����n��N*����Cn+1��Cn������������ڣ�����˵�ֵ���������ڣ�˵�����ɣ�
��1����֤������{an}Ϊ�Ȳ����У�����{an}��ͨ�ʽ��
��2����bn=2n•an��������{bn}��ǰn���Tn��
��3����Cn=4n+��-1��n-1•��2an����Ϊ����������n��N*�����Ƿ����ȷ���˵�ֵ��ʹ�ö�����n��N*����Cn+1��Cn������������ڣ�����˵�ֵ���������ڣ�˵�����ɣ�
���㣺���е����,���е���ʽ
ר�⣺�Ȳ�������ȱ�����
��������1�����õ���ʽ���Ȳ����е�ͨ�ʽ���ɵó���
��2�����á���λ����������ȱ����е�ǰn���ʽ���ɵó���
��3���ɣ�1���ɵã�Cn=4n+��-1��n-1��2n+1��������ڦ�ʹ�ö�����n��N*����Cn+1��Cn�������Cn+1-Cn=4n+1+��-1��n��2n+2-[4n+��-1��n-1•�ˡ�2n+1]����Ϊ��-1��n-1•�ˣ�2n-1��������Ԧ˷������ۣ����ɵó���
��2�����á���λ����������ȱ����е�ǰn���ʽ���ɵó���
��3���ɣ�1���ɵã�Cn=4n+��-1��n-1��2n+1��������ڦ�ʹ�ö�����n��N*����Cn+1��Cn�������Cn+1-Cn=4n+1+��-1��n��2n+2-[4n+��-1��n-1•�ˡ�2n+1]����Ϊ��-1��n-1•�ˣ�2n-1��������Ԧ˷������ۣ����ɵó���
���
��1��֤��������֪��Sn+1+Sn-1=2Sn+1��n��2��n��N*����Sn+2+Sn=2Sn+1+1��
��an+2+an=2an+1��
��n=2ʱ��S3+S1=2S2+1��
��2a1+a2+a3=2a1+2a2+1��a3=a2+1=4��
��2a2=a1+a3=6��
����ʽ����n=1ʱҲ������
������{an}Ϊ�Ȳ����У�����Ϊ2������Ϊ1��
��an=2+��n-1��=n+1��
��2���⣺�ɣ�1��bn=2n•an=��n+1��•2n��
������{bn}��ǰn���Tn=2��2+3��22+4��23+��+��n+1����2n��
2Tn=2��22+3��23+4��24+��+n��2n+��n+1����2n+1��
��-Tn=2��2+22+23+��+2n-��n+1����2n+1=2+
-��n+1����2n+1=-n��2n+1��
��Tn=n��2n+1��
��3���ɣ�1���ɵã�Cn=4n+��-1��n-1•��2an=4n+��-1��n-1��2n+1��
������ڦ�ʹ�ö�����n��N*����Cn+1��Cn�������
Cn+1-Cn=4n+1+��-1��n��2n+2-[4n+��-1��n-1•�ˡ�2n+1]����Ϊ��-1��n-1•�ˣ�2n-1�������
��������nΪ����ʱ�����ˣ�2n-1�������
���ҽ���n=1ʱ��2n-1����СֵΪ1����ˣ�1��
��������nΪż��ʱ�����ˣ�-2n-1�������
���ҽ���n=2ʱ���ˣ�-2n-1�������
���ҽ���n=2ʱ��-2n-1�����ֵ-2��
��ˣ�-2����-2���ˣ�1���֦�Ϊ�������������=-1��
�������������ڦ�=-1��ʹ�ö�����n��N*������Cn+1��Cn��
��an+2+an=2an+1��
��n=2ʱ��S3+S1=2S2+1��
��2a1+a2+a3=2a1+2a2+1��a3=a2+1=4��
��2a2=a1+a3=6��
����ʽ����n=1ʱҲ������
������{an}Ϊ�Ȳ����У�����Ϊ2������Ϊ1��
��an=2+��n-1��=n+1��
��2���⣺�ɣ�1��bn=2n•an=��n+1��•2n��
������{bn}��ǰn���Tn=2��2+3��22+4��23+��+��n+1����2n��
2Tn=2��22+3��23+4��24+��+n��2n+��n+1����2n+1��
��-Tn=2��2+22+23+��+2n-��n+1����2n+1=2+
| 2(2n-1) |
| 2-1 |
��Tn=n��2n+1��
��3���ɣ�1���ɵã�Cn=4n+��-1��n-1•��2an=4n+��-1��n-1��2n+1��
������ڦ�ʹ�ö�����n��N*����Cn+1��Cn�������
Cn+1-Cn=4n+1+��-1��n��2n+2-[4n+��-1��n-1•�ˡ�2n+1]����Ϊ��-1��n-1•�ˣ�2n-1�������
��������nΪ����ʱ�����ˣ�2n-1�������
���ҽ���n=1ʱ��2n-1����СֵΪ1����ˣ�1��
��������nΪż��ʱ�����ˣ�-2n-1�������
���ҽ���n=2ʱ���ˣ�-2n-1�������
���ҽ���n=2ʱ��-2n-1�����ֵ-2��
��ˣ�-2����-2���ˣ�1���֦�Ϊ�������������=-1��
�������������ڦ�=-1��ʹ�ö�����n��N*������Cn+1��Cn��
���������⿼���˵���ʽ��Ӧ�á��Ȳ����е�ͨ�ʽ������λ����������ȱ����е�ǰn���ʽ�������˷������۵�˼�뷽������������������������������������⣮

��ϰ��ϵ�д�
�����Ŀ
��x2��x1��1������
| A��e x1-x2��lgx1-lgx2 | ||
B��e
| ||
| C��x1 x2��x2 x1 | ||
| D��x1 x2��x2 x1 |
Բ�������SAB�DZ߳�Ϊ2�ĵȱ������Σ�OΪ��������ģ�MΪSO���е㣬����P��Բ�����ڣ�����Բ�ܣ����� AM��MP�����P�γɵĹ켣�ij���Ϊ��������
A��
| ||||
B��
| ||||
C��
| ||||
D��
|
ִ����ͼ��ʾ�ij����ͼ���������x��ֵΪ-
���������i��ֵΪ��������
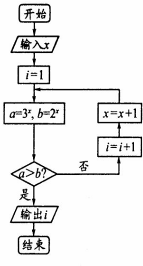
| 3 |
| 2 |

| A��4 | B��3 | C��2 | D��1 |
 ��ͼ��ij������̨���ֵĸ���ͼ����A��B��C��D��E���������װ��3�ֲ�ͬ�����й�ɽˮ��������������й�ɽˮ����ͬ����ͬ��װ�ѷ�������
��ͼ��ij������̨���ֵĸ���ͼ����A��B��C��D��E���������װ��3�ֲ�ͬ�����й�ɽˮ��������������й�ɽˮ����ͬ����ͬ��װ�ѷ�������