题目内容
设函数f（x）=|x+2|+|2x-4|，g（x）=a+x．（Ⅰ）当a=3时，解不等式f（x）≥g（x）；
（Ⅱ）画出函数y=f（x）的图象，根据图象求使f（x）≥g（x）恒成立的实数a的取值范围．
考点：绝对值不等式的解法,指数函数的图像变换
专题：不等式的解法及应用
分析：（Ⅰ）当a=3时，化简函数f（x）的解析式，分类讨论求得不等式f（x）≥g（x）的解集．
（2）画出函数f（x）的图象，数形结合求得f（x）的最小值为f（2）=4，由题意可得f（2）≥g（2），由此求得a的范围．
（2）画出函数f（x）的图象，数形结合求得f（x）的最小值为f（2）=4，由题意可得f（2）≥g（2），由此求得a的范围．
解答：
解：（Ⅰ）当a=3时，函数f（x）=|x+2|+|2x-4|=
，
不等式即f（x）≥x+3．
∴
①或
②或
③．
解①求得x＜-2，解②求得-2≤x≤
，解③求得x≥
，
综上可得，不等式的解集为（-∞，
]∪[
，+∞）．
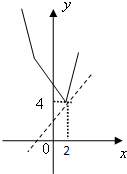
（2）根据f（x）的解析式，画出函数f（x）的图象，如图所示：
数形结合求得f（x）的最小值为f（2）=4，由于g（x）=a+x结合由题意可得f（2）≥g（2），即4≥a+2，求得a≤2．
解：（Ⅰ）当a=3时，函数f（x）=|x+2|+|2x-4|=
|
不等式即f（x）≥x+3．
∴
|
|
|
解①求得x＜-2，解②求得-2≤x≤
| 3 |
| 2 |
| 5 |
| 2 |
综上可得，不等式的解集为（-∞，
| 3 |
| 2 |
| 5 |
| 2 |
（2）根据f（x）的解析式，画出函数f（x）的图象，如图所示：
数形结合求得f（x）的最小值为f（2）=4，由于g（x）=a+x结合由题意可得f（2）≥g（2），即4≥a+2，求得a≤2．
点评：本题主要考查带有绝对值的函数，函数的恒成立问题，绝对值不等式的解法，体现了转化、数形结合、分类讨论的数学思想，属于中档题．
练习册系列答案
相关题目
下列结论中正确的是（ ）
| A、若两个变量的线性相关性越强，则相关系数的绝对值越接近于0 |
| B、在某项测量中，测量结果ξ服从正态分布N（1，σ2）（σ＞0），若ξ位于区域（0，1）的概率为0.4，则ξ位于区域（1，+∞）内的概率为0.6 |
| C、从匀速传递的产品生产流水线上，质检员每4'分钟从中抽取一件产品进行某项指标检测，这样的抽样是分层抽样 |
| D、利用随机变量Χ2来判断“两个独立事件X，Y的关系”时，算出的Χ2值越大，判断“X与Y有关”的把握就越大 |
函数f（x）、g（x）的图象在区间[a，b]上连续不断，且f′（x）•g（x）＞f（x）•g′（x），g（x）＞0，则对任意的x∈（a，b）都有（ ）
| A、f（x）•g（x）＞f（a）•g（b） |
| B、f（x）•g（a）＞f（a）•g（x） |
| C、f（x）•g（x）＞f（b）•g（b） |
| D、f（x）•g（b）＞f（b）•g（x） |
若已知α∈（-
，0），且sin（π-α）=log8
，则cos（2π-α）的值等于（ ）
| π |
| 2 |
| 1 |
| 4 |
A、
| ||||
B、-
| ||||
C、±
| ||||
D、
|
若α是第四象限角，则（ ）
| A、sinα＞tanα |
| B、sinα＜tanα |
| C、sinα≥tanα |
| D、以上都不对 |
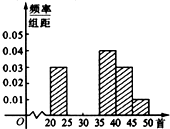某校开展校园文化活动，其中一项是背诵古诗100首，在该项进行一段时间后，随机抽取40人，统计调查了他们会背古诗的首数，得到的数据如下：已知圆C：x2+y2=4，若点P（x0，y0）在圆C外，则直线l：x0x+y0y=4与圆C的位置关系为（ ）
| A、相离 | B、相切 |
| C、相交 | D、不能确定 |