题目内容
16.在区间[0,1]上任取两个实数a,b,则函数f(x)=$\frac{1}{3}$x2+ax-b在区间[-1,1]上有且仅有一个零点的概率为$\frac{7}{9}$.分析 本题考查的知识点是几何概型的意义,关键是要找出函数 f(x)=$\frac{1}{3}$x3+ax-b在区间[-1,1]上有且仅有一个零点时(a,b)点对应的图形的面积,并将其代入几何概型的计算公式,进行求解.
解答 解:若函数 f(x)=$\frac{1}{3}$x3+ax-b在区间[-1,1]上有且仅有一个零点.
则f(-1)•f(1)≤0,
即(-$\frac{1}{3}$-a-b)•($\frac{1}{3}$+a-b)≤0,
即b≤a+$\frac{1}{3}$,
如下图,满足条件的(a,b)落在阴影上, ,
,
∵S阴影=1-$\frac{1}{2}$•($\frac{2}{3}$)2=$\frac{7}{9}$,
故答案为:$\frac{7}{9}$.
点评 几何概型的概率估算公式中的“几何度量”,可以为线段长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.解决的步骤均为:求出满足条件A的基本事件对应的“几何度量”N(A),再求出总的基本事件对应的“几何度量”N,最后根据P=$\frac{N(A)}{N}$求解.

练习册系列答案
相关题目
6.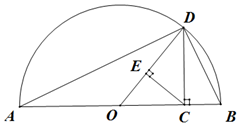 若a>0,b>0,则称$\frac{2ab}{a+b}$为a,b的调和平均数.如图,点C为线段AB上的点,且AC=a,BC=b,点O为线段AB中点,以AB为直径做半圆,过点C作AB的垂线交半圆于D,连结OD,AD,BD.过点C作OD的垂线,垂足为E,则图中线段OD的长度是a,b的算术平均数,那么图中表示a,b的几何平均数与调和平均数的线段,以及由此得到的不等关系分别是( )
若a>0,b>0,则称$\frac{2ab}{a+b}$为a,b的调和平均数.如图,点C为线段AB上的点,且AC=a,BC=b,点O为线段AB中点,以AB为直径做半圆,过点C作AB的垂线交半圆于D,连结OD,AD,BD.过点C作OD的垂线,垂足为E,则图中线段OD的长度是a,b的算术平均数,那么图中表示a,b的几何平均数与调和平均数的线段,以及由此得到的不等关系分别是( )
 若a>0,b>0,则称$\frac{2ab}{a+b}$为a,b的调和平均数.如图,点C为线段AB上的点,且AC=a,BC=b,点O为线段AB中点,以AB为直径做半圆,过点C作AB的垂线交半圆于D,连结OD,AD,BD.过点C作OD的垂线,垂足为E,则图中线段OD的长度是a,b的算术平均数,那么图中表示a,b的几何平均数与调和平均数的线段,以及由此得到的不等关系分别是( )
若a>0,b>0,则称$\frac{2ab}{a+b}$为a,b的调和平均数.如图,点C为线段AB上的点,且AC=a,BC=b,点O为线段AB中点,以AB为直径做半圆,过点C作AB的垂线交半圆于D,连结OD,AD,BD.过点C作OD的垂线,垂足为E,则图中线段OD的长度是a,b的算术平均数,那么图中表示a,b的几何平均数与调和平均数的线段,以及由此得到的不等关系分别是( )| A. | $CD,CE,\frac{2ab}{a+b}≥\sqrt{ab}$ | B. | $CD,DE,\frac{2ab}{a+b}≤\sqrt{ab}$ | C. | $CD,CE,\frac{2ab}{a+b}≥\sqrt{ab}$ | D. | $CD,CE,\frac{2ab}{a+b}≤\sqrt{ab}$ |
5.在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为矩形,AB=2BC,E是CD上一点,若AE⊥平面PBD,则$\frac{CE}{ED}$的值为( )
| A. | $\frac{3}{2}$ | B. | $\frac{5}{2}$ | C. | 3 | D. | 4 |