题目内容
20.若定义在R上的函数f(x)满足:(Ⅰ)f(x1+x2)=f(x1)•f(x2),(Ⅱ)?x1<x2,f(x1)>f(x2),则满足以上条件的一个函数解析式为y=($\frac{1}{3}$)x.分析 根据题意,由(Ⅰ)的运算律分析可得此函数为指数函数,由(Ⅱ)可得该函数为减函数,由于符合此条件的函数很多,从中择一作为答案即可.
解答 解:根据题意,对于(Ⅰ)f(x1+x2)=f(x1)•f(x2),任意一个指数函数均符合(Ⅰ);
(Ⅱ)?x1<x2,f(x1)>f(x2),则函数f(x)为减函数,
由上,符合上述两条件的函数关系式必为一个底数在(0,1)上的指数型函数,
则可知满足以上条件的一个函数解析式为y=($\frac{1}{3}$)x
故答案为:y=($\frac{1}{3}$)x.(答案不唯一,只要是底数在(0,1)上的指数函数就正确)
点评 本题考查指数函数的性质,关键是由(Ⅰ)分析得到要求函数应该为指数函数.

练习册系列答案
相关题目
5.在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为矩形,AB=2BC,E是CD上一点,若AE⊥平面PBD,则$\frac{CE}{ED}$的值为( )
| A. | $\frac{3}{2}$ | B. | $\frac{5}{2}$ | C. | 3 | D. | 4 |
12.设数列{an}的前n项和为Sn,a4=7且4Sn=n(an+an+1),则a5等于( )
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
9.${∫}_{0}^{\frac{π}{6}}$cosxdx=${∫}_{1}^{a}$$\frac{1}{x}$dx(a>1),则a的值为( )
| A. | $\sqrt{e}$ | B. | 2 | C. | e | D. | 3 |
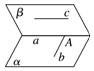 如图,已知平面α∩平面β=直线a,直线b?α,直线c?β,b∩a=A,c∥a.求证:b与c是异面直线.
如图,已知平面α∩平面β=直线a,直线b?α,直线c?β,b∩a=A,c∥a.求证:b与c是异面直线.