题目内容
已知f（x+1）-f（x）=2，f（1）=1，则f（x）= ．
考点：函数解析式的求解及常用方法
专题：计算题,函数的性质及应用
分析：由f（x+1）-f（x）=2，得f（2）-f（1）=2，f（3）-f（2）=2，f（4）-f（3）=2，…，f（x）-f（x-1）=2，以上各式累加可求．
解答：
解：已知f（x+1）-f（x）=2，
则：f（2）-f（1）=2，
f（3）-f（2）=2，
f（4）-f（3）=2，
…
f（x）-f（x-1）=2，
叠加：f（x）-f（x-1）+f（x-1）-f（x-2）+…+f（4）-f（3）+f（3）-f（2）+f（2）-f（1）=2（x-1），
∴f（x）-f（1）=2x-2，
又f（1）=1，
∴f（x）=2x-1．
则：f（2）-f（1）=2，
f（3）-f（2）=2，
f（4）-f（3）=2，
…
f（x）-f（x-1）=2，
叠加：f（x）-f（x-1）+f（x-1）-f（x-2）+…+f（4）-f（3）+f（3）-f（2）+f（2）-f（1）=2（x-1），
∴f（x）-f（1）=2x-2，
又f（1）=1，
∴f（x）=2x-1．
点评：该题考查函数解析式的求解及常用方法，注意累加法适用的题目特征．
练习册系列答案
学练快车道口算心算速算天天练系列答案
相关题目
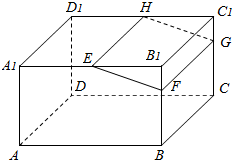如图，在长方体ABCD-A1B1C1D1中，E、H分别是棱A1B1，D1C1上的点（点E与B1不重合），且EH∥A1D1，过EH的平面与棱BB1，CC1相交，交点分别为F，G
将甲，乙两名同学5次物理测验的成绩用茎叶图表示如图，若甲，乙两人成绩的中位数分别是x甲，x乙，下列说法正确的是（ ）| A、x甲＜x乙，乙比甲成绩稳定 |
| B、x甲＞x乙；甲比乙成绩稳定 |
| C、x甲＞x乙；乙比甲成绩稳定 |
| D、x甲＜x乙；甲比乙成绩稳定 |