题目内容
6.已知方程$\frac{{x}^{2}}{1+k}-\frac{{y}^{2}}{1-k}$=1表示双曲线,则k的取值范围是-1<k<1.分析 利用双曲线的性质,列出不等式求解即可.
解答 解:因为方程$\frac{{x}^{2}}{1+k}-\frac{{y}^{2}}{1-k}$=1表示双曲线方程,所以(1-k)(1+k)>0,解得-1<k<1.
故答案为:-1<k<1
点评 本题考查双曲线的简单性质的应用,考查计算能力.

练习册系列答案
相关题目
14.设a,b∈R,定义运算“∨”和“∧”如下:$a∨b=\left\{\begin{array}{l}b,a≤b\\ a,a>b\end{array}\right.$,$a∧b=\left\{\begin{array}{l}a,a≤b\\ b,a>b\end{array}\right.$,若正数a,b,c,d满足ab≤4,c+d≥4,则( )
| A. | a∧b≥2,c∧d≥2 | B. | a∧b≤2,c∨d≥2 | C. | a∨b≥2,c∧d≤2 | D. | a∨b≤2,c∨d≤2 |
1.设随机变量X的分布列如下:
其中a,b,c,成等差数列,若E(X)=$\frac{1}{3}$,则D(X)的值是( )
| X | -1 | 0 | 1 |
| P | a | b | c |
| A. | $\frac{5}{9}$ | B. | $\frac{5}{8}$ | C. | $\frac{3}{8}$ | D. | $\frac{7}{9}$ |
15.已知α,β均为锐角,且$sinα=\frac{1}{2}sin({α+β})$,则α,β的大小关系是( )
| A. | α<β | B. | α>β | C. | α=β | D. | 不确定 |
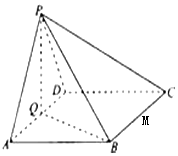 如图,四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q是AD的中点.
如图,四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q是AD的中点.