题目内容
已知函数y=f(x)的图象如图,则以下四个函数y=f(-x),y=-f(x),y=f(|x|)与y=|f(x)|的图象分别和上面四个图的正确对应关系是( )


| A、①②④③ | B、①②③④ |
| C、④③②① | D、④③①② |
考点:函数的图象
专题:数形结合,函数的性质及应用
分析:y=f(-x)与函数y=f(x)的图象关于y轴对称;y=-f(x)与函数y=f(x)的图象关于x轴对称;要得到y=f(|x|)的图象,可将y=f(x),x≤0的部分作出,再利用偶函数的图象关于y轴的对称性,作出x<0的图象即可;要得到y=|f(x)|的图象,可将y=f(x)的图象在x轴下方的部分以x轴为对称轴翻折到x轴上方,其余部分不变即可;
解答:
解:由对称变换规律知:
y=f(-x)与函数y=f(x)的图象关于y轴对称;
y=-f(x)与函数y=f(x)的图象关于x轴对称;
要得到y=f(|x|)的图象,可将y=f(x),x≤0的部分作出,再利用偶函数的图象关于y轴的对称性,作出x<0的图象即可;
要得到y=|f(x)|的图象,可将y=f(x)的图象在x轴下方的部分以x轴为对称轴翻折到x轴上方,其余部分不变即可;
故选:A.
y=f(-x)与函数y=f(x)的图象关于y轴对称;
y=-f(x)与函数y=f(x)的图象关于x轴对称;
要得到y=f(|x|)的图象,可将y=f(x),x≤0的部分作出,再利用偶函数的图象关于y轴的对称性,作出x<0的图象即可;
要得到y=|f(x)|的图象,可将y=f(x)的图象在x轴下方的部分以x轴为对称轴翻折到x轴上方,其余部分不变即可;
故选:A.
点评:本题考查函数的图象、函数的图象与图象变化,考查学生读图能力,分析问题解决问题的能力,属于基础题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
空间4点A,B,C,D共面但不共线,下列结论中正确的是( )
| A、4点中必能找出其中3点共线 |
| B、4点中必能找出其中3点不共线 |
| C、AB,BC,CD,DA中必有两条平行 |
| D、AB与CD必相交 |
若函数g(x)=x2+2x-12m在区间(-∞,-2)与(-2,1)上各有一个实根,则实数m的取值范围是( )
A、(-∞,
| ||
B、(
| ||
C、(0,
| ||
D、(
|
甲、乙两人在一次射击比赛中各射靶5次,两人成绩的条形统计图如图所示,则( )


| A、甲的成绩的平均数小于乙的成绩的平均数 |
| B、甲的成绩的方差小于乙的成绩的方差 |
| C、甲的成绩的中位数等于乙的成绩的中位数 |
| D、甲的成绩的极差小于乙的成绩的极差 |
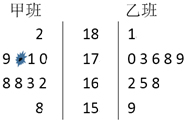 随机抽取某中学高三年级甲乙两班各10名同学,测量出他们的身高(单位:cm),获得身高数据的茎叶图如图.其中甲班有一个数据被污损.
随机抽取某中学高三年级甲乙两班各10名同学,测量出他们的身高(单位:cm),获得身高数据的茎叶图如图.其中甲班有一个数据被污损. 在如图所示的茎叶图中,甲、乙两组数据的中位数分别是
在如图所示的茎叶图中,甲、乙两组数据的中位数分别是