题目内容
10.已知双曲线 $C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的右焦点为F,双曲线C与过原点的直线相交于A、B两点,连接AF,BF.若|AF|=6,|BF|=8,$cos∠BAF=\frac{3}{5}$,则该双曲线的离心率为5.分析 在△AFB中,由余弦定理可得|BF|2=|AB|2+|AF|2-2|AB|•|AF|cos∠BAF,即可得到|AB|,由勾股定理的逆定理,可得∠ABF=90°,设F′为双曲线的右焦点,连接BF′,AF′.根据对称性可得四边形AFBF′是矩形.即可得到a,c,进而求得离心率.
解答 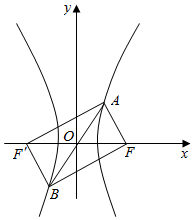 解:在△AFB中,由余弦定理可得
解:在△AFB中,由余弦定理可得
|BF|2=|AB|2+|AF|2-2|AB|•|AF|cos∠BAF,
即有64=|AB|2+36-12|AB|•
化为|AB|2-$\frac{36}{5}$|AB|-28=0,
解得|AB|=10.
由勾股定理的逆定理,可得∠ABF=90°,
设F'为双曲线的右焦点,连接BF′,AF′.
根据对称性可得四边形AFBF′是矩形.
结合矩形性质可知,2c=10,利用双曲线定义,2a=8-6=2,
所以离心率e=$\frac{c}{a}$=5.
故答案为:5.
点评 熟练掌握余弦定理、双曲线的定义、对称性、离心率、矩形的性质等基础知识是解题的关键,考查运算能力,属于中档题.

练习册系列答案
相关题目
9.已知点A是抛物线C:x2=2py(p>0)上一点,O为坐标原点,若A,B是以点M(0,10)为圆心,|OA|的长为半径的圆与抛物线C的两个公共点,且△ABO为等边三角形,则p的值是( )
| A. | $\frac{5}{2}$ | B. | $\frac{5}{3}$ | C. | $\frac{5}{6}$ | D. | $\frac{5}{9}$ |
5.双曲线a2x2-$\frac{a}{3}$y2=1的一个焦点是(-2,0),则a等于( )
| A. | -$\frac{1}{4}$ | B. | 1 | C. | -$\frac{1}{4}$或1 | D. | $\frac{1}{4}$或-1 |
20.F为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的右焦点,点P在双曲线右支上,△POF(O为坐标原点)满足OF=OP=5,$P{F_{\;}}=2\sqrt{5}$,则双曲线的离心率为 ( )
| A. | $\sqrt{3}+1$ | B. | $\sqrt{5}$ | C. | 2 | D. | $\sqrt{3}$ |
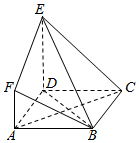 如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.
如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.