题目内容
11.双曲线x2-2y2=1的渐近线方程为y=±$\frac{\sqrt{2}}{2}$x.分析 将双曲线的方程化为标准方程,求得a,b,由渐近线方程为y=±$\frac{b}{a}$x,即可得到所求方程.
解答 解:双曲线x2-2y2=1即为
x2-$\frac{{y}^{2}}{\frac{1}{2}}$=1,
可得a=1,b=$\frac{\sqrt{2}}{2}$,
渐近线方程为y=±$\frac{b}{a}$x,
即为y=±$\frac{\sqrt{2}}{2}$x.
故答案为:y=±$\frac{\sqrt{2}}{2}$x.
点评 本题考查双曲线的渐近线方程的求法,注意运用双曲线的方程和渐近线的方程的关系,考查运算能力,属于基础题.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
16.已知双曲线C:$\frac{{y}^{2}}{2}$-$\frac{{x}^{2}}{b}$=1(b>0)的离心率为2,则C上任意一点到两条渐近线的距离之积为( )
| A. | $\sqrt{2}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | 3 |
3.如果双曲线经过点P(2,$\sqrt{2}$),且它的一条渐近线方程为y=x,那么该双曲线的方程是( )
| A. | x2-$\frac{3{y}^{2}}{2}$=1 | B. | $\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{2}$=1 | C. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{6}$=1 | D. | $\frac{{y}^{2}}{2}$-$\frac{{x}^{2}}{2}$=1 |
20.F为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的右焦点,点P在双曲线右支上,△POF(O为坐标原点)满足OF=OP=5,$P{F_{\;}}=2\sqrt{5}$,则双曲线的离心率为 ( )
| A. | $\sqrt{3}+1$ | B. | $\sqrt{5}$ | C. | 2 | D. | $\sqrt{3}$ |
1.已知函数f(x)=xsinx+cosx+x2,则不等式$f(lnx)+f(ln\frac{1}{x})<2f(1)$的解集为( )
| A. | (e,+∞) | B. | (0,e) | C. | $(0,\frac{1}{e})∪(1,e)$ | D. | $(\frac{1}{e},e)$ |
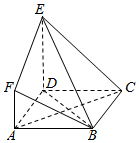 如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.
如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.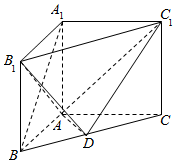 如图,在直三棱柱ABC-A1B1C1中,点D是BC的中点,AB⊥AC,AB=3,AC=4,AA1=BC.
如图,在直三棱柱ABC-A1B1C1中,点D是BC的中点,AB⊥AC,AB=3,AC=4,AA1=BC.