题目内容
14.经过双曲线$\frac{x^2}{9}-\frac{y^2}{16}=1$的左顶点、虚轴上端点、右焦点的圆的方程是x2+y2-2x+$\frac{1}{4}$y-15=0.分析 求出双曲线的左顶点、虚轴上端点、右焦点的坐标,利用待定系数法进行求解即可.
解答 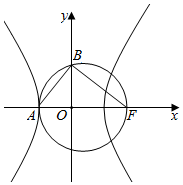 解:双曲线的左顶点A(-3,0)、虚轴上端点B(0,4)、右焦点F(5,0),
解:双曲线的左顶点A(-3,0)、虚轴上端点B(0,4)、右焦点F(5,0),
设圆的一般方程为x2+y2+Dx+Ey+F=0,
则$\left\{\begin{array}{l}{9-3D+F=0}\\{16+4E+F=0}\\{25+5D+F=0}\end{array}\right.$,得D=-2,E=$\frac{1}{4}$,F=-15,
即圆的一般方程为x2+y2-2x+$\frac{1}{4}$y-15=0,
故答案为:x2+y2-2x+$\frac{1}{4}$y-15=0
点评 本题主要考查双曲线的图象和性质以及圆的方程的求解,利用待定系数法是解决本题的关键.

练习册系列答案
相关题目
5.双曲线a2x2-$\frac{a}{3}$y2=1的一个焦点是(-2,0),则a等于( )
| A. | -$\frac{1}{4}$ | B. | 1 | C. | -$\frac{1}{4}$或1 | D. | $\frac{1}{4}$或-1 |
9.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的一条渐近线方程为y=2x,则双曲线的离心率为( )
| A. | $\sqrt{5}$ | B. | $\frac{{\sqrt{5}}}{2}$ | C. | $\sqrt{5}$或$\frac{{\sqrt{5}}}{2}$ | D. | 2 |
3.如果双曲线经过点P(2,$\sqrt{2}$),且它的一条渐近线方程为y=x,那么该双曲线的方程是( )
| A. | x2-$\frac{3{y}^{2}}{2}$=1 | B. | $\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{2}$=1 | C. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{6}$=1 | D. | $\frac{{y}^{2}}{2}$-$\frac{{x}^{2}}{2}$=1 |
4.已知双曲线的一个焦点F,点P在双曲线的一条渐近线上,点O为双曲线的对称中心,若△OFP为等腰直角三角形,则双曲线的离心率为( )
| A. | $\sqrt{6}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $\sqrt{3}$ |
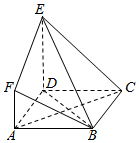 如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.
如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.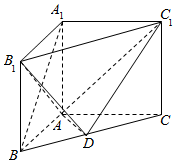 如图,在直三棱柱ABC-A1B1C1中,点D是BC的中点,AB⊥AC,AB=3,AC=4,AA1=BC.
如图,在直三棱柱ABC-A1B1C1中,点D是BC的中点,AB⊥AC,AB=3,AC=4,AA1=BC.