题目内容
7.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的一个实轴端点与恰与抛物线y2=-4x的焦点重合,且双曲线的离心率等于2,则该双曲线的方程为( )| A. | $\frac{x^2}{4}-\frac{y^2}{12}=1$ | B. | $\frac{x^2}{12}-\frac{y^2}{4}=1$ | C. | $\frac{x^2}{3}-\frac{y^2}{1}=1$ | D. | ${x^2}-\frac{y^2}{3}=1$ |
分析 求出抛物线的焦点,可得a=1,运用离心率公式可得c=2,求得b,即可得到所求双曲线的方程.
解答 解:抛物线y2=-4x的焦点为(-1,0),
由题意可得a=1,
双曲线的离心率等于2,即有
e=$\frac{c}{a}$=2,解得c=2,
b=$\sqrt{{c}^{2}-{a}^{2}}$=$\sqrt{3}$,
即有双曲线的方程为x2-$\frac{{y}^{2}}{3}$=1.
故选:D.
点评 本题考查双曲线的方程的求法,注意运用抛物线的焦点和双曲线的离心率公式,考查运算能力,属于基础题.

练习册系列答案
相关题目
6.已知抛物线C:y2=2px(p>0)的焦点为F,点A,B在C上,且点F是△AOB的重心,则cos∠AFB为( )
| A. | -$\frac{3}{5}$ | B. | -$\frac{7}{8}$ | C. | -$\frac{11}{12}$ | D. | -$\frac{23}{25}$ |
12.双曲线x2-$\frac{{y}^{2}}{4}$=1的渐近线方程为( )
| A. | y=±4x | B. | y=±2x | C. | y=±$\frac{1}{2}x$ | D. | y=±$\frac{1}{4}$x |
16.已知双曲线C:$\frac{{y}^{2}}{2}$-$\frac{{x}^{2}}{b}$=1(b>0)的离心率为2,则C上任意一点到两条渐近线的距离之积为( )
| A. | $\sqrt{2}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | 3 |
17.已知双曲线M:x2-$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的左、右焦点分别为F1,F2,过点F1与双曲线的一条渐近线平行的直线与另一条渐近线交于点P,若点P在以原点为圆心,双曲线M的虚轴长为半径的圆内,则b2的取值范围是( )
| A. | (7+4$\sqrt{3}$,+∞) | B. | (7-4$\sqrt{3}$,+∞) | C. | (7-4$\sqrt{3}$,7+4$\sqrt{3}$) | D. | (0,7-4$\sqrt{3}$)∪(7+4$\sqrt{3}$,+∞) |
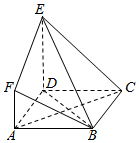 如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.
如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.