题目内容
不等式|x-1|+|2x-1|>a恒成立,则实数a的取值范围是 .
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:通过对x范围的分类讨论,可求得f(x)=|x-1|+|2x-1|=
的最小值,从而可得实数a的取值范围.
|
解答:
解:∵f(x)=|x-1|+|2x-1|=
,
∴当x<
时,f(x)=2-3x为(-∞,
)上的减函数,故f(x)>f(
)=
;
当
≤x≤1时,f(x)=x,
≤f(x)≤1;
当x>1时,f(x)=3x-2为(1,+∞)上的增函数,故f(x)>1;
综上所述,f(x)min=
,
∵不等式|x-1|+|2x-1|>a恒成立,
∴a<f(x)min=
,
∴实数a的取值范围是(-∞,
).
故答案为:(-∞,
).
|
∴当x<
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
当
| 1 |
| 2 |
| 1 |
| 2 |
当x>1时,f(x)=3x-2为(1,+∞)上的增函数,故f(x)>1;
综上所述,f(x)min=
| 1 |
| 2 |
∵不等式|x-1|+|2x-1|>a恒成立,
∴a<f(x)min=
| 1 |
| 2 |
∴实数a的取值范围是(-∞,
| 1 |
| 2 |
故答案为:(-∞,
| 1 |
| 2 |
点评:本题考查绝对值不等式的解法,求得f(x)=|x-1|+|2x-1|=
的最小值是关键,考查分类讨论思想与运算求解能力,属于中档题.
|

练习册系列答案
相关题目
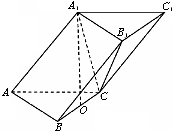 在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=
在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=