题目内容
lgx2=6-（|x|-2010）（|x|-2012）的解的个数为 ．
考点：函数零点的判定定理
专题：函数的性质及应用
分析：本题即求 函数y=6-lgx2 与 y=（|x|-2010）（|x|-2012）的交点的个数．由于这两个函数都是偶函数，图象关于y轴对称，只要求出当x＞0时的交点个数，再乘以2即得所求．结合图象可得结论
解答：
解：方程lgx2=6-（|x|-2010）（|x|-2012）的解的个数
即 函数y=6-lgx2 与 y=（|x|-2010）（|x|-2012）的交点的个数．
由于这两个函数都是偶函数，图象关于y轴对称，
只要求出当x＞0时的交点个数，再乘以2即得所求．
当x＞0时，
这两个函数的解析式即y=6-2lgx，y=（x-2010）（x-2012），
如图所示：
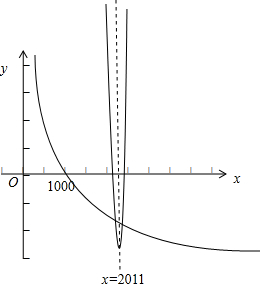
故当x＞0时，
这两个函数的解析式即y=6-2lgx 与y=（x-2010）（x-2012）有3个交点，
（注意二次函数的图象可与y轴相交，而y=6-2lgx 的图象不与y轴相交），
故方程lgx2=6-（|x|-2010）（|x|-2012）的解的个数为6，
故答案为：6个．
即 函数y=6-lgx2 与 y=（|x|-2010）（|x|-2012）的交点的个数．
由于这两个函数都是偶函数，图象关于y轴对称，
只要求出当x＞0时的交点个数，再乘以2即得所求．
当x＞0时，
这两个函数的解析式即y=6-2lgx，y=（x-2010）（x-2012），
如图所示：
故当x＞0时，
这两个函数的解析式即y=6-2lgx 与y=（x-2010）（x-2012）有3个交点，
（注意二次函数的图象可与y轴相交，而y=6-2lgx 的图象不与y轴相交），
故方程lgx2=6-（|x|-2010）（|x|-2012）的解的个数为6，
故答案为：6个．
点评：本题主要考查方程的根的存在性及个数判断，函数的奇偶性的应用，体现了化归与转化、数形结合的数学思想，属于中档题
练习册系列答案
教学练新同步练习系列答案
课前课后同步练习系列答案
课堂小作业系列答案
黄冈小状元口算速算练习册系列答案
相关题目
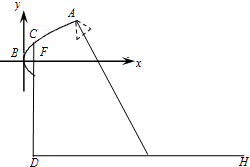为了迎接青奥会，南京将在主干道统一安装某种新型节能路灯，该路灯由灯柱和支架组成．在如图所示的直角坐标系中，支架ACB是抛物线y2=2x的一部分，灯柱CD经过该抛物线的焦点F且与路面垂直，其中C在抛物线上，B为抛物线的顶点，DH表示道路路面，BF∥DH，A为锥形灯罩的顶，灯罩轴线与抛物线在A处的切线垂直．安装时要求锥形灯罩的顶到灯柱的距离是1.5米，灯罩的轴线正好通过道路路面的中线．