题目内容
给出以下四个命题:
①已知命题p:?x∈R,tanx=2;命题q:?x∈R,x2-x+1≥0.则命题p∧q是真命题;
②圆C1:x2+y2+2x=0与圆C2:x2+y2+2y-1=0恰有2条公切线;
③在某项测量中,测量结果ξ服从正态分布N(1,σ2)(σ>0).若ξ在(0,1)内取值的概率为0.4,则ξ在(0,2)内取值的概率为0.8;
④某企业有职工150人,其中高级职称15人,中级职称45人,一般职员90人,若用分层抽样的方法抽出一个容量为30的样本,则一般职员抽出20人.
其中正确命题的序号为 (把你认为正确的命题序号都填上)
①已知命题p:?x∈R,tanx=2;命题q:?x∈R,x2-x+1≥0.则命题p∧q是真命题;
②圆C1:x2+y2+2x=0与圆C2:x2+y2+2y-1=0恰有2条公切线;
③在某项测量中,测量结果ξ服从正态分布N(1,σ2)(σ>0).若ξ在(0,1)内取值的概率为0.4,则ξ在(0,2)内取值的概率为0.8;
④某企业有职工150人,其中高级职称15人,中级职称45人,一般职员90人,若用分层抽样的方法抽出一个容量为30的样本,则一般职员抽出20人.
其中正确命题的序号为
考点:命题的真假判断与应用
专题:简易逻辑
分析:由正切函数的值域判断p为真,通过配方判断q为真,则命题p∧q是真命题;
由两圆的圆心距和半径间的关系判断两圆位置关系,从而得到两圆公切线条数;
直接由正态分布的对称性求得ξ在(0,2)内取值的概率判断③;
由分层抽样所抽取的比利数相等计算抽取的一般职员人数判断④.
由两圆的圆心距和半径间的关系判断两圆位置关系,从而得到两圆公切线条数;
直接由正态分布的对称性求得ξ在(0,2)内取值的概率判断③;
由分层抽样所抽取的比利数相等计算抽取的一般职员人数判断④.
解答:
解:对于①,∵tanx的值域为R,
∴命题p:?x∈R,tanx=2为真命题,
∵x2-x+1=(x-
)2+
>0,
∴命题q:?x∈R,x2-x+1≥0为真命题.
∴命题p∧q是真命题.
命题①正确;
对于②,圆C1:x2+y2+2x=0的圆心坐标为(-1,0),半径为1,
圆C2:x2+y2+2y-1=0的圆心坐标为(0,-1),半径为
.
∵两圆圆心距为
,满足
-1<
<
+1.
∴两圆相交,恰有两条公切线.
命题②正确;
对于③,ξ服从正态分布N(1,σ2),ξ在(0,1)内的概率为0.4,
由正态分布的对称性可知ξ在(1,2)内的取值概率也为0.4,
∴P(0<ξ<2)=P(0<ξ<1)+P(1<ξ<2)=0.4+0.4=0.8.
命题③正确;
对于④,根据分层抽样的定义和方法,抽取的一般职员人数为30×
=18,
命题④错误.
∴正确命题的序号是①②③.
故答案为:①②③.
∴命题p:?x∈R,tanx=2为真命题,
∵x2-x+1=(x-
| 1 |
| 2 |
| 3 |
| 4 |
∴命题q:?x∈R,x2-x+1≥0为真命题.
∴命题p∧q是真命题.
命题①正确;
对于②,圆C1:x2+y2+2x=0的圆心坐标为(-1,0),半径为1,
圆C2:x2+y2+2y-1=0的圆心坐标为(0,-1),半径为
| 2 |
∵两圆圆心距为
| 2 |
| 2 |
| 2 |
| 2 |
∴两圆相交,恰有两条公切线.
命题②正确;
对于③,ξ服从正态分布N(1,σ2),ξ在(0,1)内的概率为0.4,
由正态分布的对称性可知ξ在(1,2)内的取值概率也为0.4,
∴P(0<ξ<2)=P(0<ξ<1)+P(1<ξ<2)=0.4+0.4=0.8.
命题③正确;
对于④,根据分层抽样的定义和方法,抽取的一般职员人数为30×
| 90 |
| 150 |
命题④错误.
∴正确命题的序号是①②③.
故答案为:①②③.
点评:本题考查命题的真假判断与应用,考查了圆与圆的位置关,考查了服从正态分布的概率的求法,在分层抽样中,要注意每层所抽取的比例数相等,是中档题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
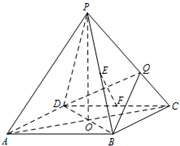 如图,正四棱锥P-ABCD的高为PO,PO=AB=2.E,F分别是棱PB,CD的中点,Q是棱PC上的点.
如图,正四棱锥P-ABCD的高为PO,PO=AB=2.E,F分别是棱PB,CD的中点,Q是棱PC上的点. 如图,△ABC内接于⊙O,AB=AC,点D在⊙O上,AD⊥AB,AD交BC于点E,点F在DA的延长线上,AF=AE,求证:
如图,△ABC内接于⊙O,AB=AC,点D在⊙O上,AD⊥AB,AD交BC于点E,点F在DA的延长线上,AF=AE,求证: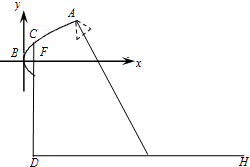 为了迎接青奥会,南京将在主干道统一安装某种新型节能路灯,该路灯由灯柱和支架组成.在如图所示的直角坐标系中,支架ACB是抛物线y2=2x的一部分,灯柱CD经过该抛物线的焦点F且与路面垂直,其中C在抛物线上,B为抛物线的顶点,DH表示道路路面,BF∥DH,A为锥形灯罩的顶,灯罩轴线与抛物线在A处的切线垂直.安装时要求锥形灯罩的顶到灯柱的距离是1.5米,灯罩的轴线正好通过道路路面的中线.
为了迎接青奥会,南京将在主干道统一安装某种新型节能路灯,该路灯由灯柱和支架组成.在如图所示的直角坐标系中,支架ACB是抛物线y2=2x的一部分,灯柱CD经过该抛物线的焦点F且与路面垂直,其中C在抛物线上,B为抛物线的顶点,DH表示道路路面,BF∥DH,A为锥形灯罩的顶,灯罩轴线与抛物线在A处的切线垂直.安装时要求锥形灯罩的顶到灯柱的距离是1.5米,灯罩的轴线正好通过道路路面的中线.