题目内容

已知正实数x，y满足条件
1
2x+1
+
1
y+1
=
4
7
，则xy的最小值是
 
．
考点：基本不等式
专题：导数的综合应用,不等式的解法及应用
分析：由于正实数x，y满足条件
1
2x+1
+
1
y+1
=
4
7
，可得y=
6x+10
8x-3
＞0，x＞
3
8
．于是xy=
x(6x+10)
8x-3
=
6x2+10x
8x-3
=f（x），再利用导数研究函数的单调性极值与最值即可得出．
解答： 解：∵正实数x，y满足条件
1
2x+1
+
1
y+1
=
4
7
，可得y=
6x+10
8x-3
＞0，解得x＞
3
8
．
∴xy=
x(6x+10)
8x-3
=
6x2+10x
8x-3
=f（x），
则f′（x）=
(12x+10)(8x-3)-8(6x2+10x)
(8x-3)2
=
48x2-36x-30
(8x-3)2
=
6(2x+1)(4x-5)
(8x-3)2
，
当且仅当x=
5
4
时，函数f（x）取得最小值，f(
5
4
)=
6×(
5
4
)2+10×
5
4
8×
5
4
-3
=
25
8
．
故答案为：
25
8
．
点评：本题考查了利用导数研究函数的单调性极值与最值，属于中档题．
练习册系列答案
相关题目
已知矩阵A
-1   0
0     2
，B=
1   2
0   6
，则矩阵A-1B=
 
．
若x＞0，y＞0，且
1
x
+
4
y
=1，则xy的最小值为
 
．
设Z1=i4+i5+i6+…+i12，Z2=i4•i5•i6•…•i12，则Z1，Z2关系为
 
．
若从1，2，3，…，9这9个整数中同时取4个不同的数，其和为偶数，则不同的取法共有
 
．
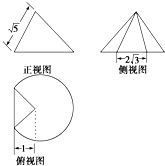一个圆锥被过其顶点的一个平面截去了较少的一部分几何体，余下的几何体的三视图如图，则余下部分的几何体的体积为（　　）
A、
16π
9
B、
16π
9
+
2
3
3
C、
8π
9
+
3
3
D、
16π
3
+2
3
下面给出了四个推理：
①由（1+1）2＞21，（2+1）2＞22，（3+1）2＞23，…，归纳：对一切n∈N*，（n+1）2＞2n；
②已知△ABC周长为c，且它的内切圆半径为r，则三角形的面积为
1
2
cr，类比：若四面体D-ABC的表面积
为s，内切球半径为r，则其体积是
1
3
sr；
③“若a，b∈R，则a-b＞0⇒a＞b”，类比：“若a，b∈C，（C为复数集）则a-b＞0⇒a＞b”；
④由圆x2+y2=r2的面积s=πr2，类比：椭圆
x2
a2
+
y2
b2
=1的面积s=πab．
上述四个推理中，结论正确的是（　　）
A、①②B、②③C、②④D、③④
已知F是抛物线y=
1
8
x2的焦点，P是该抛物线上的动点，则PF中点的轨迹方程是（　　）
A、x2-4y+2=0
B、2x2-8y+1=0
C、x2-4y+4=0
D、2x2-8y+6=0
如图，A1B1C1-ABC是三棱柱，下列直线中与AA1成异面直线的是（　　）
A、BB1
B、CC1
C、B1C1
D、AB

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网