题目内容
12.下列图象可以作为函数f(x)=$\frac{x}{{x}^{2}+a}$的图象的有( )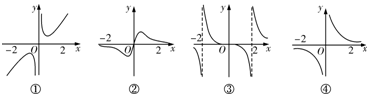
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 通过a与0的大小,分类讨论,通过函数的奇偶性判断求解即可.
解答 解:当a<0时,如取a=-4,则f(x)=$\frac{x}{{x}^{2}-4}$,其定义域为:{x|x≠±2},它是奇函数,图象是③,所以③选项是正确的;
当a>0时,如取a=1,其定义域为R,它是奇函数,图象是②.所以②选项是正确的;
当a=0时,则f(x)=$\frac{1}{x}$,其定义域为:{x|x≠0},它是奇函数,图象是④,所以④选项是正确的.
故选:C.
点评 本题考查函数的图象的判断,考查分类讨论思想的应用,函数的奇偶性的判断,是中档题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
3.某班级有学生50名,班主任为了检查学生的学习状况,用系统抽样方法从中抽取10人,将这50名学生随机编号为1~50号,若36号被抽到了,则下列编号的学生被抽到的是( )
| A. | 4 | B. | 17 | C. | 28 | D. | 41 |
20.A={x|y=lg(x-1)},$B=\left\{{y\left|{y=\sqrt{4-{x^2}}}\right.}\right\}$,则A∩B=( )
| A. | [0,2] | B. | (1,2] | C. | [1,2) | D. | (1,4] |
17.一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如表(单位:辆):
按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
(Ⅰ)求z的值;
(Ⅱ)用分层抽样的方法在C类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
(Ⅲ)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分x的值如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2,把这8辆轿车的得分看成一个总体,从中任取一个数xi(1≤i≤8,i∈N),设样本平均数为$\overline{x}$,求|xi-$\overline{x}$|≤0.5的概率.
| 轿车A | 轿车B | 轿车C | |
| 舒适型 | 100 | 150 | z |
| 标准型 | 300 | 450 | 600 |
(Ⅰ)求z的值;
(Ⅱ)用分层抽样的方法在C类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
(Ⅲ)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分x的值如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2,把这8辆轿车的得分看成一个总体,从中任取一个数xi(1≤i≤8,i∈N),设样本平均数为$\overline{x}$,求|xi-$\overline{x}$|≤0.5的概率.
1.在三棱锥P-ABC中,PA=4,∠PBA=∠PCA=90°,△ABC是边长为2的等边三角形,则三棱锥P-ABC的外接球球心到平面ABC的距离是( )
| A. | $\frac{{2\sqrt{6}}}{3}$ | B. | $\frac{{\sqrt{33}}}{3}$ | C. | $\frac{{4\sqrt{6}}}{3}$ | D. | $\frac{{2\sqrt{33}}}{3}$ |
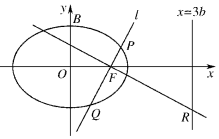 已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),点F,B分别是椭圆的右焦点与上顶点,O为坐标原点,记△OBF的周长与面积分别为C和S.
已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),点F,B分别是椭圆的右焦点与上顶点,O为坐标原点,记△OBF的周长与面积分别为C和S.