题目内容
1.在三棱锥P-ABC中,PA=4,∠PBA=∠PCA=90°,△ABC是边长为2的等边三角形,则三棱锥P-ABC的外接球球心到平面ABC的距离是( )| A. | $\frac{{2\sqrt{6}}}{3}$ | B. | $\frac{{\sqrt{33}}}{3}$ | C. | $\frac{{4\sqrt{6}}}{3}$ | D. | $\frac{{2\sqrt{33}}}{3}$ |
分析 由圆周角定理及球的性质可判断PA为球的直径,利用余弦定理求出PA与平面ABC所成角的大小,即可得出球心到平面ABC的距离.
解答 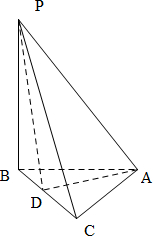 解:∵∠PBA=∠PCA=90°,
解:∵∠PBA=∠PCA=90°,
∴PA为平面PAB所在圆的截面的直径,
同理PA也是PBC所在圆的截面的直径,
∴PA的中点为外接球的球心,
由勾股定理得PB=PC=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
取BC的中点D,连接AD,
则∠PAD为PA与平面ABC所成的角,
经计算得AD=$\sqrt{3}$,PD=$\sqrt{11}$,
∴cos∠PAD=$\frac{16+3-11}{2×4×\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴sin∠PAD=$\frac{\sqrt{6}}{3}$,
∴球心O到平面ABC的距离d=$\frac{1}{2}$PAsin∠PAD=$\frac{2\sqrt{6}}{3}$.
故选A.
点评 本题考查了棱锥的结构特征,棱锥与外接球的关系,属于中档题.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
17.如果x,y满足$\left\{{\begin{array}{l}{2x-y+1≤0}\\{x-y+1≥0}\\{2x+y+5≥0}\end{array}}\right.$,则$z=\frac{x+2y-3}{x+1}$的取值范围是( )
| A. | $({-∞,-\frac{8}{5}}]∪[{3,+∞})$ | B. | $[{-1,\frac{1}{7}}]$ | C. | (-1,0]∪[3,+∞) | D. | (-∞,-1]∪[7,+∞) |
12.下列图象可以作为函数f(x)=$\frac{x}{{x}^{2}+a}$的图象的有( )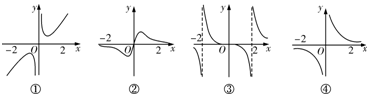

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
9.已知f(x)=ax2+(b-a)x+c-b(其中a>b>c),若a+b+c=0,x1、x2为f(x)的两个零点,则|x1-x2|的取值范围为( )
| A. | ($\frac{3}{2}$,2$\sqrt{3}$) | B. | (2,2$\sqrt{3}$) | C. | (1,2) | D. | (1,2$\sqrt{3}$) |