题目内容
如图,水以常速(即单位时间内注入水的体积相同)注入下面四种底面积相同的容器中,请分别找出与各容器对应的水的高度h与时间l的函数关系图象.则对应正确的是( )
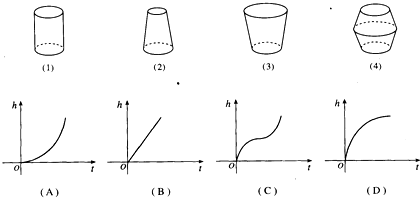

| A、(1)→(B),(2)→(A),(3)→(C),(4)→(D) |
| B、(1)→(A),(2)→(B),(3)→(D),(4)→(C) |
| C、(1)→(D),(2)→(A),(3)→(B),(4)→(C) |
| D、(1)→(B),(2)→(A),(3)→(D),(4)→(C) |
考点:函数的图象
专题:函数的性质及应用
分析:结合几何体的结构和题意知,容器的底面积越大水的高度变化慢、反之变化的快,再由图象越平缓就是变化越慢、图象陡就是变化快来判断.
解答:
解:因为图(1)是圆柱体,故水面高度的增加是均匀的,即图象是直线型的,所以所对应的图象为B;
图(2)因几何体下面宽上面窄,且相同的时间内注入的水量相同,所以下面的高度增加的慢,上面增加的快,即图象应越来越陡,所以所对应的图象为A;
图(3)因几何体下面窄上面宽,且相同的时间内注入的水量相同,所以下面的高度增加的快,上面增加的慢,即图象应越来平缓,所以所对应的图象为D;
图(3)图中几何体两头窄、中间宽,所以水的高度增加的先快后慢最后再快,则图象先平缓再变陡,所以所对应的图象为C;
故选:D
图(2)因几何体下面宽上面窄,且相同的时间内注入的水量相同,所以下面的高度增加的慢,上面增加的快,即图象应越来越陡,所以所对应的图象为A;
图(3)因几何体下面窄上面宽,且相同的时间内注入的水量相同,所以下面的高度增加的快,上面增加的慢,即图象应越来平缓,所以所对应的图象为D;
图(3)图中几何体两头窄、中间宽,所以水的高度增加的先快后慢最后再快,则图象先平缓再变陡,所以所对应的图象为C;
故选:D
点评:本题考查了数形结合思想,对于此题没有必要求容器中水面的高度h和时间t之间的函数解析式,因此可结合几何体和图象作定性分析,即充分利用数形结合思想.

练习册系列答案
相关题目
在平行四边形ABCD中,AC为一条对角线,若
=(2,4),
=(1,3),则
=( )
| AB |
| AC |
| BD |
| A、(2,4) |
| B、(-2,-4) |
| C、(3,5) |
| D、(-3,-5) |
向所示图中边长为2的正方形中,随机撒一粒黄豆,则黄豆落在图中阴影部分的概率为( )


A、
| ||
B、
| ||
C、
| ||
D、
|
不等式(x-1)(2-x)≥0的解集是( )
| A、{x|1≤x≤2} |
| B、{x|x≥2或x≤1} |
| C、{x|1<x<2} |
| D、{x|x>2或x<1} |
若a<
,则化简
的结果是( )
| 1 |
| 4 |
| 4 | (4a-1)2 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|