题目内容
向所示图中边长为2的正方形中,随机撒一粒黄豆,则黄豆落在图中阴影部分的概率为( )


A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:概率与统计
分析:利用定积分公式,求出阴影部分的面积,代入几何概型概率计算公式,可得答案.
解答:
解:阴影部分的面积S=2×
+
dx=1+2ln2,
边长为2的正方形的面积为:4,
故随机撒一粒黄豆,则黄豆落在图中阴影部分的概率P=
,
故选:A
| 1 |
| 2 |
| ∫ | 2
|
| 1 |
| x |
边长为2的正方形的面积为:4,
故随机撒一粒黄豆,则黄豆落在图中阴影部分的概率P=
| 1+2ln2 |
| 4 |
故选:A
点评:本题考查的知识点是几何概型,其中利用定积分公式,求出阴影部分的面积,是解答的关键,难度中档.

练习册系列答案
相关题目
如图所示的程序框图中输出的a的结果为( )


| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
设等差数列{an}的前n项和为Sn,若a11-a8=3,则使S11-S8=3,最小正整数an>0的值是( )
| A、8 | B、9 | C、11 | D、10 |
如图,水以常速(即单位时间内注入水的体积相同)注入下面四种底面积相同的容器中,请分别找出与各容器对应的水的高度h与时间l的函数关系图象.则对应正确的是( )
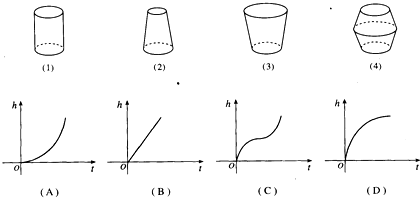

| A、(1)→(B),(2)→(A),(3)→(C),(4)→(D) |
| B、(1)→(A),(2)→(B),(3)→(D),(4)→(C) |
| C、(1)→(D),(2)→(A),(3)→(B),(4)→(C) |
| D、(1)→(B),(2)→(A),(3)→(D),(4)→(C) |