题目内容
已知二次函数f(x)=ax2+bx+c的图象的最高点的坐标是(2,3),且与x轴的交点中,有一个交点的横坐标为1,求f(x)的表达式.
考点:函数解析式的求解及常用方法,二次函数的性质
专题:计算题,函数的性质及应用
分析:由题意设f(x)=a(x-2)2+3,从而解得f(x)=-3(x-2)2+3.
解答:
解:∵二次函数f(x)=ax2+bx+c的图象的最高点的坐标是(2,3),
∴f(x)=a(x-2)2+3;
代入f(1)=a(1-2)2+3=0;
解得a=-3;
故f(x)=-3(x-2)2+3.
∴f(x)=a(x-2)2+3;
代入f(1)=a(1-2)2+3=0;
解得a=-3;
故f(x)=-3(x-2)2+3.
点评:本题考查了函数的解析式的求法与应用,属于基础题.

练习册系列答案
相关题目
如图,水以常速(即单位时间内注入水的体积相同)注入下面四种底面积相同的容器中,请分别找出与各容器对应的水的高度h与时间l的函数关系图象.则对应正确的是( )
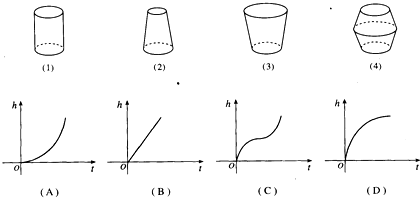

| A、(1)→(B),(2)→(A),(3)→(C),(4)→(D) |
| B、(1)→(A),(2)→(B),(3)→(D),(4)→(C) |
| C、(1)→(D),(2)→(A),(3)→(B),(4)→(C) |
| D、(1)→(B),(2)→(A),(3)→(D),(4)→(C) |
在命题“方程x2=4的解是x=±2”中,逻辑联结词的使用情况是( )
| A、使用了逻辑联结词“或” |
| B、使用了逻辑联结词“且” |
| C、使用了逻辑联结词“非” |
| D、未使用逻辑联结词“或”、“且”、“非” |
以下有关命题的说法正确的是( )
| A、命题“若x2-3x+2=0则x=1或x=2”的逆否命题为“若x≠1或x≠2,则x2-3x+2≠0” | ||||
| B、若p∧q为假命题,则p、q均为假命题 | ||||
C、“9<k<25”是“方程
| ||||
| D、对于命题p:?x∈R使得x2+x+1<0,则¬p:?x∈R,均有x2+x+1≥0 |