题目内容
已知sin（α+
）+sin（α-
）=
，则
的值为 ．
| π |
| 4 |
| π |
| 4 |
| ||
| 3 |
sin(α-
| ||
| 1-cos2α-sin2α |
考点：两角和与差的正弦函数,同角三角函数基本关系的运用
专题：三角函数的求值
分析：将已知条件化简整理，可得sinα=
，再利用两角差的正弦与二倍角的正弦与余弦公式将所求关系式进行化简整理，即可求得答案．
| 1 |
| 3 |
解答：
解：∵sin（α+
）+sin（α-
）=2sinαcos
=
sinα=
，
∴sinα=
．
∴
=
=
=
，
故答案为：
．
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 2 |
| ||
| 3 |
∴sinα=
| 1 |
| 3 |
∴
sin(α-
| ||
| 1-cos2α-sin2α |
| ||||||||
| 2sin2α-2sinαcosα |
| ||||
| 2sinα |
3
| ||
| 4 |
故答案为：
3
| ||
| 4 |
点评：本题考查两角差的正弦与二倍角的正弦与余弦公式的综合应用，考察化简、运算能力，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
如图，水以常速（即单位时间内注入水的体积相同）注入下面四种底面积相同的容器中，请分别找出与各容器对应的水的高度h与时间l的函数关系图象．则对应正确的是（ ）
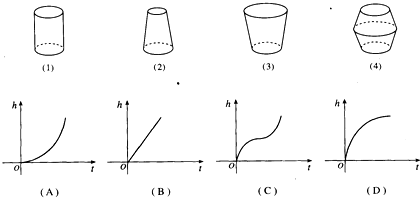
| A、（1）→（B），（2）→（A），（3）→（C），（4）→（D） |
| B、（1）→（A），（2）→（B），（3）→（D），（4）→（C） |
| C、（1）→（D），（2）→（A），（3）→（B），（4）→（C） |
| D、（1）→（B），（2）→（A），（3）→（D），（4）→（C） |
在命题“方程x2=4的解是x=±2”中，逻辑联结词的使用情况是（ ）
| A、使用了逻辑联结词“或” |
| B、使用了逻辑联结词“且” |
| C、使用了逻辑联结词“非” |
| D、未使用逻辑联结词“或”、“且”、“非” |
已知数列
，
，
，
，…那么它的一个通项公式是（ ）
| 3 |
| 2 |
| 4 |
| 3 |
| 5 |
| 4 |
| 6 |
| 5 |
A、an=
| ||
B、an=
| ||
C、an=
| ||
D、an=
|
若复数z与其共轭复数
满足|z|=2，z+
=-2，则z=（ ）
. |
| z |
. |
| z |
A、-1+
| ||
B、-1-
| ||
C、-1±
| ||
D、-1±
|