题目内容
 已知椭圆C:
已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| 6 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)过椭圆的右焦点F的直线l1与椭圆交于A,B,过F与直线l1垂直的直线l2与椭圆交于C,D,与直线l2:x=4交于交于P,求四边形ABCD面积的最小值.
考点:直线与圆锥曲线的关系,椭圆的标准方程
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)椭圆C:
+
=1(a>b>0)的离心率为
,可得a2=
b2,利用椭圆的短半轴为半径的圆与直线x-y+
=0相切,求出b,即可求椭圆C的方程;
(Ⅱ)分类讨论,设出方程代入椭圆方程,利用基本不等式,即可求四边形ABCD面积的最小值.
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| 4 |
| 3 |
| 6 |
(Ⅱ)分类讨论,设出方程代入椭圆方程,利用基本不等式,即可求四边形ABCD面积的最小值.
解答:
解:(Ⅰ)∵椭圆C:
+
=1(a>b>0)的离心率为
,
∴
=
,∴a2=
b2,
∵椭圆的短半轴为半径的圆与直线x-y+
=0相切.
∴b=
=
,
∴a2=4,b2=3
∴椭圆的方程为
+
=1;
(Ⅱ)①斜率不存在时,方程为x=1,
代入椭圆方程可得y=±
,
∴|AB|=3,|CD|=2a=4,
∴四边形ABCD面积为
×3×4=6;
斜率不为0时,方程为y=k(x-1),
代入椭圆方程可得(4k2+3)x2-8k2x+4k2-12=0
设A(x1,y1),B(x2,y2),则x1+x2=
,x1x2=
,
∴|AB|=
|x1-x2|=
,
同理|CD|=
,
∴
+
=
+
=
≥2
,
∴|AB||CD|≥
,
∴SABCD=
|AB||CD|≥
×
=
,
∵
<6,
∴四边形ABCD面积的最小值为
.
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
∴
| a2-b2 |
| a2 |
| 1 |
| 4 |
| 4 |
| 3 |
∵椭圆的短半轴为半径的圆与直线x-y+
| 6 |
∴b=
| ||
|
| 3 |
∴a2=4,b2=3
∴椭圆的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)①斜率不存在时,方程为x=1,
代入椭圆方程可得y=±
| 3 |
| 2 |
∴|AB|=3,|CD|=2a=4,
∴四边形ABCD面积为
| 1 |
| 2 |
斜率不为0时,方程为y=k(x-1),
代入椭圆方程可得(4k2+3)x2-8k2x+4k2-12=0
设A(x1,y1),B(x2,y2),则x1+x2=
| 8k2 |
| 4k2+3 |
| 4k2-12 |
| 4k2+3 |
∴|AB|=
| 1+k2 |
| 12(1+k2) |
| 3+4k2 |
同理|CD|=
| 12(1+k2) |
| 4+3k2 |
∴
| 1 |
| |AB| |
| 1 |
| |CD| |
| 12(1+k2) |
| 3+4k2 |
| 12(1+k2) |
| 4+3k2 |
| 7 |
| 12 |
|
∴|AB||CD|≥
| 122×4 |
| 49 |
∴SABCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 122×4 |
| 49 |
| 288 |
| 49 |
∵
| 288 |
| 49 |
∴四边形ABCD面积的最小值为
| 288 |
| 49 |
点评:本题考查椭圆方程,考查直线与椭圆的位置关系,考查分类讨论的数学思想,属于难题.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
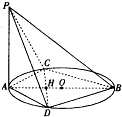 已知AB是圆O的直径,C,D是圆上不同两点,且CD∩AB=H,AC=AD,PA⊥圆O所在平面
已知AB是圆O的直径,C,D是圆上不同两点,且CD∩AB=H,AC=AD,PA⊥圆O所在平面