题目内容
如图所示，PA、PB、PC两两垂直，过P点作平面ABC的垂线，垂足为G，证明：G为△ABC的垂心．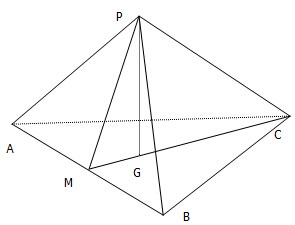
考点：直线与平面垂直的性质
专题：作图题,证明题,空间位置关系与距离
分析：连接BG，AG交AC，BC于点H，N，证明PG⊥AB，PC⊥AB，从而得证AB⊥平面PGC，则AB⊥CM．同理BH⊥AC，AN⊥BC，则G为△ABC的垂心．
解答：
证明：连接BG，AG交AC，BC于点H，N，
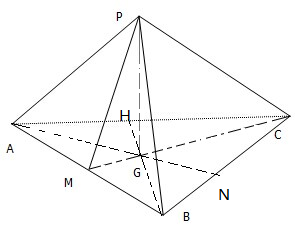∵PG⊥平面ABC，AB?平面ABC，
∴PG⊥AB，
∵PC⊥PA，PC⊥PB，PA∩PB=P，
∴PC⊥平面PAB，
又∵AB?平面ABC，
∴PC⊥AB，
∴AB⊥平面PGC，又∵CM?平面PGC，
∴AB⊥CM．
同理，BH⊥AC，AN⊥BC，
则G为△ABC的垂心．
∵PG⊥平面ABC，AB?平面ABC，∴PG⊥AB，
∵PC⊥PA，PC⊥PB，PA∩PB=P，
∴PC⊥平面PAB，
又∵AB?平面ABC，
∴PC⊥AB，
∴AB⊥平面PGC，又∵CM?平面PGC，
∴AB⊥CM．
同理，BH⊥AC，AN⊥BC，
则G为△ABC的垂心．
点评：本题考查了线面垂直的性质与判定定理，属于较基础题．
练习册系列答案
相关题目
已知椭圆C：