已知0≤x≤$\frac{3}{2}$.则函数f(x)=x2+x+1( )A．有最小值-$\frac{3}{4}$.无最大值B．有最小值$\frac{3}{4}$.最大值1C．有最小值1.最大值$\frac{19}{4}$D．无最小值和最大值题目和参考答案——青夏教育精英家教网——

题目内容

11．已知0≤x≤$\frac{3}{2}$，则函数f（x）=x²+x+1（　　）

	A．	有最小值-$\frac{3}{4}$，无最大值		B．	有最小值$\frac{3}{4}$，最大值1
	C．	有最小值1，最大值$\frac{19}{4}$		D．	无最小值和最大值

分析根据对称轴判断f（x）在[0，$\frac{3}{2}$]上的单调性，根据单调性判断最值．

解答解：f（x）=x²+x+1=（x+$\frac{1}{2}$）²+$\frac{3}{4}$，
∴f（x）在区间[0，$\frac{3}{2}$]上是增函数，
∴f（x）_min=f（0）=1，f（x）_max=f（$\frac{3}{2}$）=$\frac{19}{4}$．
故选C．

点评本题考查了二次函数的单调性，属于基础题．

练习册系列答案

优课堂给力A加系列答案

天府数学系列答案

天府前沿系列答案

文科爱好者系列答案

理科爱好者系列答案

新学案同步导与练系列答案

名师大课堂系列答案

351高效课堂导学案系列答案

状元成才路状元导练系列答案

快乐小博士巩固与提高系列答案

相关题目

1．曲线f（x）=$\frac{2}{{{x^2}-1}}$、直线x=2、x=3以及x轴所围成的封闭图形的面积是（　　）

$ln\frac{3}{2}$

2．若函数y=f（x）的定义域为R，对于?x∈R，f'（x）＜e^x，且f（x+1）为偶函数，f（2）=1，则不等式f（x）＜e^x的解集为（0，+∞）．

19．有以下命题：①如果向量$\overrightarrow{a}$，$\overrightarrow{b}$与任何向量不能构成空间向量的一组基底，那么$\overrightarrow{a}$，$\overrightarrow{b}$的关系是不共线；②O，A，B，C为空间四点，且向量$\overrightarrow{OA}$，$\overrightarrow{OB}$，$\overrightarrow{OC}$不构成空间的一个基底，那么点O，A，B，C一定共面；③已知向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$是空间的一个基底，则向量$\overrightarrow{a}$+$\overrightarrow{b}$，$\overrightarrow{a}$-$\overrightarrow{b}$，$\overrightarrow{c}$，也是空间的一个基底．其中正确的命题是②③．

6．数列 {a_n}满足 a_n+1=$\frac{1}{1-{a}_{n}}$，a₁=2，则a₂₀₁₆的值是（　　）

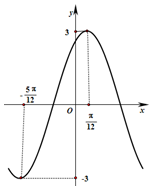函数y=Asin（ω•x+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，则此函数的解析式为y=3sin（2x+$\frac{π}{3}$）．

3．在平面直角坐标系xoy中，过点P（0，1）的直线l平分圆C：（x-2）²+y²=1的面积，则直线l的斜率k为-$\frac{1}{2}$．

20．已知f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ$＜\frac{π}{2}）$的图象过点$P（\frac{π}{3}，0）$，图象上与点P最近的一个顶点是$Q（\frac{7π}{12}，-1）$．
（I）求函数的解析式；并用“五点法”在给定的坐标系内作出函数f（x）一个周期的简图；
（II）求函数f（x）的增区间．

1．设f（x）是定义在（0，+∞）上的函数，对定义域内的任意x，y都满足f（xy）=f（x）+f（y），且x＞1时，f（x）＞0．
（1）判断f（x）在（0，+∞）上的单调性并证明；
（2）若f（2）=1，解不等式f（x）+f（x-3）≤2．