题目内容
5.已知双曲线$C:\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$满足条件:(1)焦点为F1(-5,0),F2(5,0);(2)离心率为$\frac{5}{3}$,求得双曲线C的方程为f(x,y)=0.若去掉条件(2),另加一个条件求得双曲线C的方程仍为f(x,y)=0,则下列四个条件中,①双曲线$C:\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$上的任意点P都满足||PF1|-|PF2||=6;②双曲线$C:\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$的虚轴长为4;③双曲线$C:\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$的一个顶点与抛物线y2=6x的焦点重合;④双曲线$C:\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$的渐近线方程为3x+4y=0.符合添加的条件共有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 利用已知条件求出双曲线方程,然后通过其它体积求出双曲线的标准方程,即可判断选项.
解答 解:对于①,∵||PF1|-|PF2||=2a=6,∴a=3
又∵焦点为F1(-5,0),F2(5,0),∴c=5
∴离心率e=$\frac{5}{3}$,故①符合条件;
对于②,双曲线C的虚轴长为4,∴b=2,a=$\sqrt{21}$
∴离心率e=$\frac{5}{\sqrt{21}}$,故②不符合条件;
对于③,双曲线C的一个顶点与抛物线y2=6x的焦点重合,
∴a=$\frac{3}{2}$,e=$\frac{10}{3}$,故③不符合条件;
对于④,∵渐近线方程为3x+4y=0
∴$\frac{b}{a}$=$\frac{3}{4}$,
又∵c=5,c2=a2+b2,∴a=4
∴离心率e=$\frac{5}{4}$,故④不符合条件.
故选:A.
点评 本题考查双曲线的简单性质,标准方程的求法,命题的真假的判断,是基础题.

练习册系列答案
相关题目
13.函数$f(x)=tan(ωx+\frac{π}{3})(ω>0)$的最小正周期为$\frac{π}{2}$,为了得到y=tanωx的图象,只需把y=f(x)的图象上所有点( )
| A. | 向右平移$\frac{π}{6}$个单位长度 | B. | 向右平移$\frac{π}{12}$个单位长度 | ||
| C. | 向左平移$\frac{π}{6}$个长度单位 | D. | 向左平移$\frac{π}{12}$个长度单位 |
14.已知复数$\frac{2-ai}{i}=1+bi$,其中a,b∈R,i是虚数单位,则|a+bi|=( )
| A. | -1-3i | B. | $\sqrt{5}$ | C. | 10 | D. | $\sqrt{10}$ |
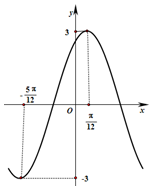 函数y=Asin(ω•x+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则此函数的解析式为y=3sin(2x+$\frac{π}{3}$).
函数y=Asin(ω•x+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则此函数的解析式为y=3sin(2x+$\frac{π}{3}$).