题目内容

6．已知函数f（x）=|x-a|+2|x+1|．
（1）当a=3时，求不等式f（x）≥6的解集；
（2）若f（x）≥4对于任意x∈R都恒成立，求实数a的取值范围．

分析 （1）利用绝对值不等式的解法，去掉绝对值，求解即可．
（2）利用f（x）min=min{f（-1），f（a）}，求解即可．

解答 解：（1）当a=3时，x＜-1，不等式可化为-3x+1≥6，∴x≤-$\frac{5}{3}$；
-1≤x≤3时，不等式可化为x+5≥6，∴x≥1，∴1≤x≤3；
当x＞3时，3x-1≥6，∴x≥$\frac{7}{3}$，∴x＞3，
综上所述，不等式的解集为{x|x≤-$\frac{5}{3}$或x≥1}；
（2）∵f（x）min=min{f（-1），f（a）}，
∴$\left\{\begin{array}{l}{f（-1）=|-1-a|≥4}\\{f（a）=2|a+1|≥4}\end{array}\right.$，∴a≤-5或a≥3．

点评 本题考查绝对值不等式的解法，考查恒成立问题，考查学生分析解决问题的能力，属于中档题．

练习册系列答案
相关题目
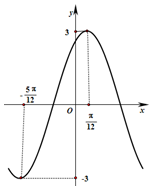16．函数y=Asin（ω•x+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，则此函数的解析式为y=3sin（2x+$\frac{π}{3}$）．
17．如果a＞b，那么下列不等式：①a3＞b3；②$\frac{1}{a}$＜$\frac{1}{b}$；③3a＞3b；④lga＞lgb．其中恒成立的是①③．
14．已知复数$\frac{2-ai}{i}=1+bi$，其中a，b∈R，i是虚数单位，则|a+bi|=（　　）
A．-1-3iB．$\sqrt{5}$C．10D．$\sqrt{10}$
1．设f（x）是定义在（0，+∞）上的函数，对定义域内的任意x，y都满足f（xy）=f（x）+f（y），且x＞1时，f（x）＞0．
（1）判断f（x）在（0，+∞）上的单调性并证明；
（2）若f（2）=1，解不等式f（x）+f（x-3）≤2．
11．函数sgn（x）=$\left\{\begin{array}{l}{-1，x＜0}\\{0，x=0}\\{1，x＞0}\end{array}$，设a=$\frac{1}{{{{log}_{\frac{1}{4}}}\frac{1}{2015}}}$+$\frac{1}{{{{log}_{\frac{1}{504}}}\frac{1}{2015}}}$，b=2017，则$\frac{a+b+（a-b）sgn（a-b）}{2}$的值为2017．
3．已知函数f（x）=me2x+nex，（m，n∈R），g（x）=x．
（1）当n=4时，若F（x）=f（x）-g（x）存在单调递增区间，求m的取值范围；
（2）当m＞0时，设f（x）图象C1与g（x）图象C2相交于不同两点M，N，过线段MN的中点P作x轴的垂线交C1于点Q（x0，y0），若记f′（x）为f（x）导数，求证：f′（x0）＜1．
20．函数f（x）=$\frac{1-x}{ax}$+lnx是[1，+∞）上的增函数．
（Ⅰ）求正实数a的取值范围；
（Ⅱ）若函数g（x）=x2+2x，在使g（x）≥M对定义域内的任意x值恒成立的所有常数M中，我们把M的最大值M=-1叫做f（x）=x2+2x的下确界，若函数f（x）=$\frac{1-x}{ax}$+lnx的定义域为[1，+∞），根据所给函数g（x）的下确界的定义，求出当a=1时函数f（x）的下确界．
（Ⅲ）设b＞0，a＞1，求证：ln$\frac{a+b}{b}$＞$\frac{1}{a+b}$．
1．已知双曲线C的方程为x2-15y2=15．其渐近线方程为y=±$\frac{\sqrt{15}}{15}$x．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网