题目内容
4.已知定义在R上的函数f(x)满足f(x)•f(x+2)=13,若f(-1)=2,则f(2013)=$\frac{13}{2}$.分析 利用题中条件:“f(x)•f(x+2)=13”得出函数f(x)是周期函数,从而利用f(1)的值求出f(2011)即可
解答 解:∵f(x)•f(x+2)=13
∴f(x+2)•f(x+4)=13,
∴f(x+4)=f(x),
∴f(x)是一个周期为4的周期函数,f(-1)•f(1)=13,f(-1)=2,
∴f(1)=$\frac{13}{2}$
∴f(2013)=f(4×503+1)=f(1)=$\frac{13}{2}$.
故答案为:$\frac{13}{2}$.
点评 本题主要考查了抽象函数及其应用,考查分析问题和解决问题的能力,属于中档题.函数的周期性是高考函数题的重点考查内容,几个重要的周期公式要熟悉,如:(1)f(x+a)=f(x-a),则T=2a;(2)f(x+a)=-$\frac{1}{f(x)}$,则T=2a等.

练习册系列答案
相关题目
12.已知奇函数f(x)满足,x>0时,f(x)=x2-2x;则x<0时,f(x)的解析式为( )
| A. | -x2-2x | B. | -x2+2x | C. | x2-2x | D. | x2+2x |
13.函数$f(x)=tan(ωx+\frac{π}{3})(ω>0)$的最小正周期为$\frac{π}{2}$,为了得到y=tanωx的图象,只需把y=f(x)的图象上所有点( )
| A. | 向右平移$\frac{π}{6}$个单位长度 | B. | 向右平移$\frac{π}{12}$个单位长度 | ||
| C. | 向左平移$\frac{π}{6}$个长度单位 | D. | 向左平移$\frac{π}{12}$个长度单位 |
14.已知复数$\frac{2-ai}{i}=1+bi$,其中a,b∈R,i是虚数单位,则|a+bi|=( )
| A. | -1-3i | B. | $\sqrt{5}$ | C. | 10 | D. | $\sqrt{10}$ |
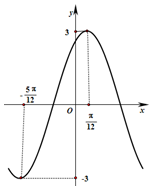 函数y=Asin(ω•x+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则此函数的解析式为y=3sin(2x+$\frac{π}{3}$).
函数y=Asin(ω•x+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则此函数的解析式为y=3sin(2x+$\frac{π}{3}$).