题目内容
6.扇形AOB的面积为4cm2,周长为10cm,求扇形中心角的弧度及弦AB的长.分析 根据题意设出扇形的弧长与半径,通过扇形的周长与面积,即可求出扇形的弧长与半径,进而根据公式α=$\frac{l}{r}$求出扇形圆心角的弧度数,利用余弦定理即可求得AB的值.
解答 解:设扇形的弧长为:l,半径为r,所以2r+l=10,
∵S扇形=$\frac{1}{2}$lr=4,
解得:r=4,l=2,
∴扇形的圆心角的弧度数是:$\frac{2}{4}$=$\frac{1}{2}$;
∴由余弦定理可得:AB=$\sqrt{16+16-2×4×4×cos\frac{1}{2}}$=4$\sqrt{2-2cos\frac{1}{2}}$.
点评 本题主要考查扇形的周长与扇形的面积公式的应用,以及考查学生的计算能力,此题属于基础题型.

练习册系列答案
相关题目
16.设f(x)=$\left\{\begin{array}{l}{x+2,(x≤0)}\\{(\frac{1}{2})^{x},(x>0)}\end{array}\right.$,则 f[f (-1)]=( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 4 |
18.已知tan(α+β-$\frac{π}{4}$)=$\frac{1}{2}$,tan(β-$\frac{π}{4}$)=-$\frac{1}{3}$,则tan(α+$\frac{π}{3}$)=( )
| A. | $\sqrt{3}$-2 | B. | 2-$\sqrt{3}$ | C. | -2+$\sqrt{3}$ | D. | -2-$\sqrt{3}$ |
2.已知函数$f(x)=\left\{{\begin{array}{l}{cosx-1,x≤0}\\{{{sin}^2}x,x>0}\end{array}}\right.$,则下列结论正确的是( )
| A. | f(x)是偶函数 | B. | f(x)是单调函数 | C. | f(x)是周期函数 | D. | f(x)的值域为[-2,1] |
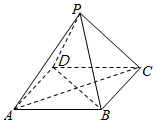 如图,已知点P是平行四边形ABCD所在平面外的一点,E、F分别是PA、BD上的点且E、F分别是PA、BD的中点.求证:EF∥平面PBC.
如图,已知点P是平行四边形ABCD所在平面外的一点,E、F分别是PA、BD上的点且E、F分别是PA、BD的中点.求证:EF∥平面PBC.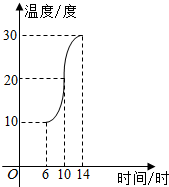 如图,某地一天从6时至14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b.
如图,某地一天从6时至14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b.