Question

15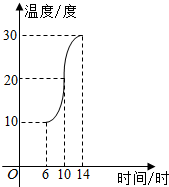．如图，某地一天从6时至14时的温度变化曲线近似满足函数y=Asin（ωx+φ）+b．
（1）求这段时间的最大温差；
（2）写出这段曲线的函数解析式．

Answer 1

分析 （1）根据函数y=Asin（ωx+φ）+b的最值求出最大温差；
（2）根据函数的最值求出A、b的值，再利用半周期求出ω与φ的值，即得函数解析式．

解答 解：（1）根据图形，得；
这段时间的最大温差为30-10=20（度）；
（2）由$\left\{\begin{array}{l}{A+b=30}\\{A-b=10}\end{array}\right.$，解得A=20，b=10；
又$\frac{1}{2}$T=$\frac{1}{2}$×$\frac{2π}{ω}$=14-6，解得ω=$\frac{π}{8}$；
当x=10时，ωx+φ=2kπ，k∈Z，
即$\frac{π}{8}$×10+φ=2kπ，k∈Z，
解得φ=2kπ-$\frac{5π}{4}$，k∈Z；
所以，这段曲线的函数解析式y=20sin（$\frac{π}{8}$x-$\frac{5π}{4}$）+10，x∈[6，14]．

点评 本题考查了利用函数y=Asin（ωx+φ）+b的部分图象求最值与解析式的应用问题，是基础题目．