题目内容
1.若复数z=$\frac{m-1}{3}$-(m-2)i(m∈R),它在复平面上对应的点为Z.则复平面上的点(1,2)到点Z之间的最短距离是$\frac{2\sqrt{10}}{5}$.分析 由题意得到复平面上点Z的参数方程,化为普通方程,由点到直线的距离公式得答案.
解答 解:设Z(x,y),
则$\left\{\begin{array}{l}{x=\frac{m-1}{3}}\\{y=2-m}\end{array}\right.$,消去m得3x+y-1=0.
则点(1,2)到直线3x+y-1=0的距离为d=$\frac{|3×1+1×2-1|}{\sqrt{{3}^{2}+{1}^{2}}}=\frac{4}{\sqrt{10}}=\frac{4\sqrt{10}}{10}=\frac{2\sqrt{10}}{5}$.
故答案为:$\frac{2\sqrt{10}}{5}$.
点评 本题考查复数的代数表示法及其几何意义,训练了点到直线的距离公式的应用,是基础题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
12.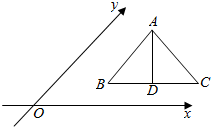 如图所示的是水平放置的三角形的直观图,D为△ABC中BC的中点,则原图形中的AB,AD,AC三条线段中( )
如图所示的是水平放置的三角形的直观图,D为△ABC中BC的中点,则原图形中的AB,AD,AC三条线段中( )
 如图所示的是水平放置的三角形的直观图,D为△ABC中BC的中点,则原图形中的AB,AD,AC三条线段中( )
如图所示的是水平放置的三角形的直观图,D为△ABC中BC的中点,则原图形中的AB,AD,AC三条线段中( )| A. | 最长的是AB,最短的是AC | B. | 最长的是AC,最短的是AB | ||
| C. | 最长的是AB,最短的是AD | D. | 最长的是AC,最短的是AD |