题目内容
设随机变量ξ的分布列为p（ξ=k）=
（k=2，4，6，8，10），则Dξ等于（ ）
| 1 |
| 5 |
| A、5 | B、10 | C、8 | D、16 |
考点：离散型随机变量及其分布列
专题：计算题,概率与统计
分析：利用数学期望、方差的计算公式即可得出．
解答：
解：根据分布列知Eξ=
（2+4+6+8+10）=6，
Dξ=
×[（2-6）2+（4-6）2+（6-6）2+（8-6）2+（10-6）2]=8
故选：C．
| 1 |
| 5 |
Dξ=
| 1 |
| 5 |
故选：C．
点评：熟练掌握数学期望、方差的计算公式是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
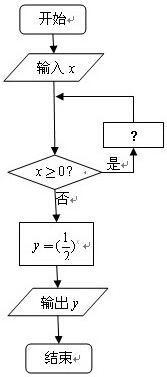执行如图程序，若输入x=10，要求输出y=4，则在图中“？”处可填入的算法语句是（ ）①x=x-1②x=x-2③x=x-3④x=x-4．
| A、①②③ | B、②③ |
| C、②③④ | D、③④ |
已知中心在原点的双曲线C的左焦点为F1（-2，0），离心率e=2，则C的标准方程是（ ）
A、x2-
| ||||
B、
| ||||
C、
| ||||
D、
|
设f（x）=
，若f（0）是f（x）的最小值，则a的取值范围为（ ）
|
| A、[-1，2] |
| B、[-1，0] |
| C、[1，2] |
| D、[0，2] |
复数z=
，|
|是（ ）
| 5 |
| 3+4i |
. |
| z |
| A、25 | B、5 | C、1 | D、7 |
结论为：xn+yn能被x+y整除，令n=1，2，3，4验证结论是否正确，得到此结论成立的条件可以为（ ）
| A、n∈N* |
| B、n∈N*且n≥3 |
| C、n为正奇数 |
| D、n为正偶数 |
函数f(x)=lnx+
的零点所在的区间是（ ）
| 1 |
| 2 |
| A、（e-4，e-2） |
| B、（e-2，1） |
| C、（1，e2） |
| D、（e2，e4） |
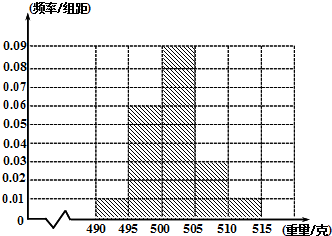某食品厂为了检查甲乙两条自动包装流水线的生产情况，随机在这两条流水线上各抽取40件产品作为样本称出它们的重量（单位：克），重量值落在（495，510]的产品为合格品，否则为不合格品．表1是甲流水线样本频数分布表，如图是乙流水线样本的频率分布直方图．