题目内容
结论为：xn+yn能被x+y整除，令n=1，2，3，4验证结论是否正确，得到此结论成立的条件可以为（ ）
| A、n∈N* |
| B、n∈N*且n≥3 |
| C、n为正奇数 |
| D、n为正偶数 |
考点：归纳推理
专题：规律型
分析：将n=1，2，3，4分别代和，可得当n为正奇数时，xn+yn能被x+y整除，当n为正偶数时xn+yn不能被x+y整除，进而得到结论．
解答：
解：当n=1时，x+y能被x+y整除，
当n=2时，x2+y2不能被x+y整除，
当n=3时，x3+y3能被x+y整除，
当n=4时，x4+y4不能被x+y整除，
…
故此结论成立的条件不应该为：n∈N*；也不应该为：n∈N*且n≥3；也不应该为：n为正偶数，
而应该为：n为正奇数，
故选：C
当n=2时，x2+y2不能被x+y整除，
当n=3时，x3+y3能被x+y整除，
当n=4时，x4+y4不能被x+y整除，
…
故此结论成立的条件不应该为：n∈N*；也不应该为：n∈N*且n≥3；也不应该为：n为正偶数，
而应该为：n为正奇数，
故选：C
点评：本题考查归纳推理的应用，其中要注意对规律的总结与归纳，大胆猜想．
练习册系列答案
英才点津系列答案
红果子三级测试卷系列答案
课堂练加测系列答案
相关题目
下列推理过程是类比推理的是（ ）
A、人们通过大量试验得出掷硬币出现正面的概率为
| ||
| B、科学家通过研究老鹰的眼睛发明了电子鹰眼 | ||
| C、通过检测溶液的pH值得出溶液的酸碱性 | ||
| D、数学中由周期函数的定义判断某函数是否为周期函数 |
函数f（x）=loga|x-1|在（0，1）上递减，那么f（x）在（1，+∞）上（ ）
| A、递增且无最大值 |
| B、递减且无最小值 |
| C、递增且有最大值 |
| D、递减且有最小值 |
设随机变量ξ的分布列为p（ξ=k）=
（k=2，4，6，8，10），则Dξ等于（ ）
| 1 |
| 5 |
| A、5 | B、10 | C、8 | D、16 |
根据图所示程序框图，当输入10时，输出的是（ ）
| A、14.1 | B、19 |
| C、12 | D、-30 |
执行如图所示的程序框图所表达的算法，输出的结果为（ ）
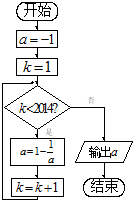
| A、2 | ||
| B、1 | ||
C、
| ||
| D、-1 |