题目内容
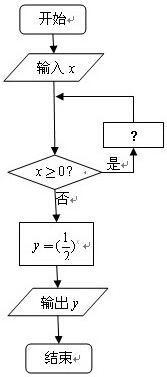 执行如图程序,若输入x=10,要求输出y=4,则在图中“?”处可填入的算法语句是( )
执行如图程序,若输入x=10,要求输出y=4,则在图中“?”处可填入的算法语句是( )①x=x-1②x=x-2③x=x-3④x=x-4.
| A、①②③ | B、②③ |
| C、②③④ | D、③④ |
考点:程序框图
专题:算法和程序框图
分析:先根据输出的y值,确定跳出循环的x值,依次判断当“?”处填①②③④时是否满足,可得答案.
解答:
解:由y=(
)x=4⇒x=-2,
∴输入x=10,当“?”处填①时,跳出循环x=0,∴①错误;
当“?”处填②时,跳出循环x=-2,∴②正确;
当“?”处填③时,跳出循环x=-2,∴③正确;
当“?”处填④时,跳出循环x=-2,∴④正确.
故选:C.
| 1 |
| 2 |
∴输入x=10,当“?”处填①时,跳出循环x=0,∴①错误;
当“?”处填②时,跳出循环x=-2,∴②正确;
当“?”处填③时,跳出循环x=-2,∴③正确;
当“?”处填④时,跳出循环x=-2,∴④正确.
故选:C.
点评:本题考查了当型循环结构的程序框图,根据框图的流程确定跳出循环的x值是解题的关键.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案
相关题目
已知tanα、tanβ是关于x的方程mx2-2x
+2m=0的两个实根,则tan(α+β)的取值范围是( )
| 7m-3 |
A、[-
| ||||||
B、[-
| ||||||
C、[-
| ||||||
D、[-
|
椭圆
+y2=1上的点到直线x-y+6=0的最小距离是( )
| x2 |
| 3 |
A、
| ||
B、2
| ||
C、3
| ||
D、4
|
如果点P(tanθ,cosθ)位于第二象限,那么以x轴非负半轴为始边的角θ的终边所在象限是( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
设角θ的终边经过点(3,-4),则sin(
-θ)的值等于( )
| π |
| 4 |
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
在△ABC中,若
=
,则△ABC的形状是( )
| a |
| cosA |
| b |
| cosB |
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰或直角三角形 |
| D、等腰直角三角形 |
设随机变量ξ的分布列为p(ξ=k)=
(k=2,4,6,8,10),则Dξ等于( )
| 1 |
| 5 |
| A、5 | B、10 | C、8 | D、16 |